Explicit Inversive Pseudorandom
Number Generators
Diplomarbeit
zur Erlangung des Magistergrades
an der Naturwissenschaftlichen Fakultät
der Universität Salzburg
eingereicht von
Otmar Lendl
Salzburg, im November 1996
Contents
As a rule, random number generators are fragile and need to be treated with
respect. It’s difficult to be sure that a particular generator is good without an
enormous amount of effort in the various statistical test.
The moral is: do your best to use a good generator, based on the mathematical
analysis and the experience of others; just to be sure, examine the numbers to
make sure that they “look” random; if anything goes wrong, blame the
random-number generator !
– Robert Sedgewick, in “Algorithms” (Second Edition, 1988)
I’d like to thank everybody who helped to make this thesis become reality. Peter
for his patience, trust and guidance; Charly, Hannes, Karin, and Stefan for the most
creative, helpful and entertaining working environment I have ever experienced; and
my mother for her unwavering support.
Chapter 1
Introduction
The purpose of this thesis is to discuss the implementation of the explicit inversive
congruential generator (EICG) and the properties of the resulting pseudorandom
numbers. But before we delve into the details of the implementation or the theoretical
and empirical results we will take a closer look at the basic concept of pseudo-random
numbers.
What do we mean when we talk about pseudorandom numbers (PRN) ? And for
what purpose do we devise such elaborate means to artificially generate megabytes of
digital noise ?
1.1 What do we need Pseudo-Random Numbers for ?
To the uninitiated, all this pseudo-random numbers “business” seems to have
no serious applications. Everybody will come up with computer games as a
field where pseudo-random numbers are used to make the behaviour of the
computer less predictable. Steering the movements of some on-screen monster
does not require a high standard of randomness, almost any algorithm will
suffice, provided it is easy to implement and does not cost too much computing
resources.
Another domain where we need PRN is wherever we need to model a more or less
random phenomenon of the real world. The simulation of a roulette table or other
forms of lottery might still be in the area of non-serious application, but here
the defects of the generator start to be an issue. Imagine this scenario: you
try to develop a winning strategy for blackjack and use a simulation to test
your algorithm. Any correlation between statistical defects and the strategy
will lead to a skewed result and may even change the sign of the expected
outcome. Playing that strategy in a real casino might cost you dearly. Thus it is
important to make the choice of the generator an issue even in such non-scientific
applications.
Simulation of random events is far from being limited to gambling, a significant
percentage of all simulations of natural phenomena contains a random component.
Whether that may be quantum effects, rainfall on a certain area, Brownian motion,
absorption pattern, bifurcation of tree roots, failure of technical components, solar
activity …, in all cases we know at best the statistical properties of an event. An
analytical solution of the given problem based on probabilities is often not possible.
Thus one has to resort to stochastic simulation (see [3, 48, 75]) where one calculates
the result of the overall simulation by choosing possible outcomes of the underlying
random events according to their respective probability. Doing this a number of times
should provide enough samples of the outcome to estimate the probability of each
possible result. Needless to say, the selection of the realisations of the underlying
random events is crucial to the correctness of the whole calculation. Since this selection
is done with the aid of PRN, their quality plays an important role in the whole
process.
Finding the use of PRN in stochastic simulation is not that surprising, but finding
them in algorithms for such mundane tasks like integration might need some more
explanation. Numerical integration is a common problem in a great deal of real world
problems. A big battery of algorithms (trapezoid method, Simpson’s method, spline
quadrature, adaptive quadrature, Runge-Kutta, …) was developed to minimize the
calculation costs while increasing the accuracy of the result. All these methods scale
very badly with the dimension of the integral, so a completely different approach is
more appropriate there. The Monte Carlo method (see [3, 48, 78, 84]) uses randomly
selected samples of the function to estimate the integral. Provided we know
more about the behaviour of the function (i.e. its total variation) and the
distribution of the actual samples used (as measured by their discrepancy), the
inequality of Koksma-Hlawka (See page , [51, 70]) will give an error bound for
this method. Since it is generally not possible to calculate the exact value of
the discrepancy of the random numbers used for the integration, this error
bound will only be a probabilistic one. In order to get a deterministic one, the
random numbers, which determine which samples of the function will be
evaluated, are replaced by numbers for which the order of the discrepancy
is known. This turns the Monte Carlo method into the Quasi-Monte Carlo
method.
One way to get such good point sets is to explicitly construct
them with that goal in mind (See [70] for a discussion of
-nets
and other methods.) or use a PRNG for which an upper bound on the discrepancy is
known. This is one of the reasons why we will take a close look at this quantity in
Section 3.3. Not all applications of Quasi-Monte Carlo integration are labeled
as such, as the basic algorithm can be regarded as a simple heuristic. For
example, distributed ray tracing [32, p. 788] uses a set of randomly distributed
rays to implement spatial and temporal antialiasing which amounts to an
integration over both the time-frame of the picture and the pixel’s spatial
extension.
Non-deterministic algorithms often use pseudorandom numbers, too. These
algorithms are used to tackle problems for which a deterministic solution takes too
much time. Although they cannot guarantee success, they promise to find the solution
(or a sub-optimal one) within reasonable time. Examples for this kind of algorithm are
Pollard’s rho heuristic [8, p. 844] for integer factorization, the Rabin-Miller
primality test [8, p. 839], Simulated Annealing [31], and Threshold Accepting
[11].
Other algorithms use pseudorandom numbers for a different purpose. Instead of
using them directly for solving the problem they are used to randomize the problem
(or the algorithm) in order to avoid running into the same worst-case behaviour again
and again. See [8, p. 161] for an explanation of the rationale behind randomized
quick-sort.
Some cryptographic algorithms and protocols require a good source of random
numbers, too. Stream ciphers [77, p. 168f], for example, use the output of a
PRNG (termed keystream generator) to encrypt the plaintext. The security of this
cipher depends largely on the statistical quality of the keystream. Any regularities of
the PRNG can be used by the attacker to predict the next bits and thus crack the
code. No other domain of PRNG applications has such a high demand on the
“randomness” of the generated PRN. Algorithms which are good enough for
stochastic simulations are typically way too predictable to be useful as a
keystream generator for a stream cipher. Thus the field of cryptographically
secure PRNG has amazingly little in common with the study of PRNG for
stochastic simulation on which we will focus in this thesis. Information on
cryptographically secure pseudorandom numbers can be found in [52], [82], and
[77].
Another application of pseudo-random numbers in the field of cryptology is
providing the “random” numbers needed for a variety of cryptographic protocols. A
well known example are the session keys generated for each transaction in hybrid
cryptosystems. As the recent debacle involving the Netscape Navigator [33, 69] has
shown, one must be very careful not to use a simple PRNG for this task. Since this is
more a matter of how to get the entropy needed for non-predictability than one of
analysing the properties of sequences of PRN we will not elaborate on this subject in
this thesis.
1.2 Criteria for PRN Generator Selection
Now that we know a bit about the various applications of PRN, let’s try to formulate
a few criteria for the selection of a good PRN generation algorithm. As we will see
later it is crucial for the selection of the right PRNG to keep an eye on the application
of the PRN.
1.2.1 Reproducibility
This criterion may sound strange at first sight, since reproducibility contradicts the
intuitive notion of randomness, and indeed, real random number generators are
extremely unlikely to ever repeat their output. So what are the advantages of a
generator which will produce the same sequence of pseudorandom numbers when fed
with the same parameters ? Once again, we have to turn to the application of which
the generator is a component. In the case of a stochastic simulation the benefit is
twofold:
- As a scientific experiment, it should be possible to redo the same calculations
under the same conditions. This ensures that an independent verification
of the obtained result is possible.
- Debugging and verifying the simulation program is greatly helped by the
possibility of replaying the calculation. Otherwise it may not be possible to
determine if an unexpected outcome is caused by a systematic error in the
simulation setup, or whether it is just a statistic fluke.
In some areas, for example stream ciphers, reproducibility is a key requirement for
the application. Only very few applications, most of them in the area of cryptography,
do actually benefit from the use of non-reproducible PRN.
1.2.2 Statistical properties
It is clear that when we want to simulate a random variable with a PRNG, then the
output of the generator should model as closely as possible the expected behaviour of
instances of the random variable. If a simulation of a dice generates a 7 or
strongly favors the 6 we will not accept the generator. Other deviations from the
desired behaviour, e.g. correlations, are harder to detect, and methods for
systematically testing generators for such deficiencies have been the subject of
considerable mathematical work [50, 28, 54, 85], including some parts of this
thesis.
As we will see later, proving that a generator really has all the statistical
properties a real random number generator is supposed to have, is not possible.
So all we can do is to establish faith in the generator by testing it for some
properties.
1.2.3 Empirical Test Results
Empirical testing usually involves using the PRN for a stochastic simulation with a
known result. If the computed results contradict the expected ones, the generator will
be dismissed as not suitable for that kind of stochastic simulation. A passed test will
increase the faith that this generator will yield correct results in real world
problems. We will examine the significance of empirical test results later in greater
details.
A large battery of such tests was developed over the years, from the well known
tests of Knuth [50] and Marsaglia [66] to recent additions like the weighted spectral
test [40, 41, 46, 44]. See [54, §3.5.] for further references on testing pseudorandom
number generators.
1.2.4 Possibility of Theoretical Analysis
In order to make analytical investigations possible, most modern PRNG are defined in
quite simple mathematical terms. It is a tradeoff: The simpler the algorithm, the easier
it will be to prove statements concerning the quality of the generated numbers. On the
other hand, a convoluted algorithm appeals to the intuition. History has shown
[50, 74] that quite a few people could not resist the temptation to build generators
based on doing obscure transformations on numbers stored in computers.
Empirical analysis has shown that the quality of such generators are often
abysmal.
1.2.5 Results of Theoretical Analysis
Doing empirical studies on the properties of a PRNG is always possible, but
deriving properties of the generator output by pure mathematical study has a
lot of advantages. Whereas an empirical test can only cover one specific set
of parameters of a generator, it is sometime possible to make analytically
proven statements on the properties of PRN generated by a certain generator
regardless of the parameters used. In the same vein, an empirical test on a specific
part of the generator’s output, say the first billion numbers, may give us
confidence on the behaviour of the next billion numbers, but cannot offer any
guarantee that they will be equally good. Analytical results fall in the following
categories:
- Basic parameter selection
For most generators not all possible parameters will result in a functional
generator. A typical question is that of gaining the largest possible period
length. For the LCG
this is just a set of simple conditions, for the ICG it involves finding IMP
polynomials [6, 30, 45, 42, 43, 25]. For compound generators to work it
is also necessary to obey certain analytically derived constraints.
- Properties of the resulting PRN
For some generators it is possible to derive statements on some aspects of
the output. The well-known fact that tuples of LCG generated numbers
form lattices (see page ) is one example.
- Estimates and bounds
Especially the discrepancy has been the subject of analytical study. There
are numerous estimates and bounds for various generators.
1.2.6 Efficiency
With all the mathematical discussions about the merits of PRN generated by a new
algorithm one should not forget the fact that we need to actually implement this
algorithm on a real computer. There are a few things which should be noted
here:
- Implementation costs
Implementing (i.e. programming) an algorithm is usually a one-time investment
of effort. Once the code is there, integrating it into a larger project is
more or less trivial. What are the difficulties in implementing a typical
pseudorandom number generation algorithm ? As we will see later in Chapter
5, the main problem lies in the handling of large integers and performing
standard mathematical operations like addition and multiplication on them.
For inversive generators finding the multiplicative inverse in
is a required operation, too.
- Computational costs
The execution of any algorithm requires both CPU and memory resources.
Typical PRNG (EICG, LCG, ICG, …) have only very small memory
requirements. The code is very compact and the state information does only
require a few bytes.
As far as CPU consumption is concerned, a PC with Intel 486DX2-66
processor is capable of executing the EICG algorithm about 70000 times in
a second. The author’s implementation of the LCG runs at about 400000
PRN per second. The highly optimized system pseudorandom number generator
runs at over 700000 calls per second. These numbers are only provided to
give a rough feeling for the speed of the algorithms when using a modulus in
the range of .
- Implications for the overall running time
As the generation of the PRN is usually performed on demand on the same
computer as the stochastic simulation for which they are used, they compete
for the same resources. The total running time for the simulation can be
described as the sum of the time used for the PRN generation plus the
time used for doing the actual calculations. The latter often dominates the
former, thus it does not make sense to try to gain overall speed by sacrificing
quality in the PRN algorithm.
1.2.7 Practical Aspects
After implementing the algorithm one has to find good parameters for that generator,
too. Fortunately, for some common PRNG tables containing suitable parameters have
been published [29, 43, 2, 83], so there is no need to reinvent the wheel there. Other
generators like the EICG are known to be rather insensitive to the choice of the
parameters.
Another aspect is the possibility to generate independent streams of pseudorandom
numbers. Such streams are needed for parallel or vectorized computing. See [55, §8],
[1], [12], and [36] for more information on this topic.
1.3 Important Types of PRN Generators
There is no shortage on proposed pseudorandom number generation algorithms. Every
year new ideas on this topic are published, but only if the resulting PRN have been
subject to intensive theoretical and empirical study the generator might have
a chance to get used in a real world problem. As it is often the case with
competing inventions, an objective technological superiority does not immediately
lead to market domination. Whether the generator is included in standard
programming libraries seems to be much more important than any published results
on the distribution properties of the numbers. A classic example is the now
infamous RANDU generator which was included in IBM’s Fortran library and
features an extremely poor distribution of triples composed of subsequent
numbers.
The following list introduces some of the most commonly used generators as well as
the inversive generators on which we will focus in this thesis. More complete surveys
on the current menagerie of PRNG can be found in [70, 72, 55].
In the following
denotes a positive integer (termed modulus) and
represents the system
of all residues modulo .
With the addition and multiplication modulo
the set
acquires
the algebraic structure of a finite ring. If the context makes it clear that we operate in the
ring
we will omit the trailing “mod”.
1.3.1 The Linear Congruential Generator
Definition 1.1 Let .
The linear congruential generator (abbreviated as “LCG”) with parameters
and
defines a sequence
in
by
and a sequence
of pseudorandom numbers in
by
As the sequence
is defined by a recursion of order one on a finite set it must be periodic. The longest possible
period length is
in the case of
and in the
case of .
The necessary conditions for achieving these period lengths are well known. [70, p.
169]
The LCG is very popular. Its implementation is quite simple, especially if
is chosen as 2 to the power of bits per native word of the computer (e.g.
) which
reduces the modulo operations to just ignoring the overflow. Due to its simplicity and
popularity the LCG has been subjected to intensive analytical and empirical examination.
The quality of the resulting PRN depends very much on the choice of the parameters
and
.
Fortunately, tables containing good parameters have been published, see [29, 27, 53].
The output of a LCG shows a strong intrinsic structure ([65], see also p.
). A number of modifications were proposed to improve the quality of the
generator. One approach is to extend the recursion to higher orders by making
a function of
. Other proposals
modify the function which describes the recursion. As the name says, the LCG uses the linear
function to
calculate
from . If we
replace
by an arbitrary function, we refer to the resulting PRNG as a general first-order
congruential generator [70, p. 177]. In order to guarantee maximal period length, the
function
must be carefully selected. For example, the quadratic congruential method, as
proposed by Knuth in [50, §3.2.2] uses a polynomial of degree 2 as the recursion and a
power of 2 as the modulus. See [70, p. 181f] for the conditions on the parameters and
analytical investigation on the resulting PRN.
1.3.2 Shift-register Generators
Shift-register generators differ from standard linear congruential generators
in two respects. First, they use a higher-order linear recursion of the form
|
| (1.1) |
where is the modulus,
is the order of the
recursion and are
elements of . Second,
instead of just scaling the
to the unity interval to get the pseudorandom numbers, the
are calculated from a block
of consecutive values .
Thus it is no longer necessary to use a large modulus to get a decent resolution of the resulting
PRN. In order to simplify and optimize the implementation of recursion, the common choice of
is the prime 2. On
a -bit computer this
allows the grouping of
steps into one operation.
Two techniques for the transformation of the sequence
into a sequence of
pseudorandom numbers in
are commonly used: The digital multistep method puts
|
| (1.2) |
The Tausworthe generator [81] is a special case of this method.
More popular is the generalized feedback shift-register method
(GSFR) which can take advantage of the above mentioned blocking of
bits if
are
selected suitably:
|
| (1.3) |
If the parameters are carefully selected the period length will in both cases be
.
Shift register pseudorandom numbers have the advantage of a fast generation
algorithm and a period length independent of the limitations of the integers used for
the calculation. See [70, Chapter 9] and [55] for a discussion on the properties of shift
register pseudorandom numbers.
1.3.3 The Inversive Congruential Generator
A promising modification of the LCG was proposed by Eichenauer
and Lehn in [14]. We will only consider the case of a prime modulus
here. It involves the operation of modular inversion in
which we will denote
by an overline ().
|
| (1.4) |
The restriction to prime moduli guarantees the unique existence of an inversive element in
. This definition
implies
for .
Definition 1.2 Let
be a (large) prime and .
The inversive congruential generator (abbreviated as “ICG”) with parameters
and
defines a sequence
in
by
and a sequence
of pseudorandom numbers in
by
Empirical as well as analytical investigations indicate that the output
of an ICG is superior to the output of a LCG in several respects: longer
usable sample sizes [85, 61], less correlations between consecutive numbers
[72].
1.3.4 The Explicit Inversive Congruential Generator
Analytical calculations have led to the following observation: We can describe the generator as a
function mapping
to . This
self-map in
the finite field
can be written as a uniquely defined polynomial
with degree
. If we demand the sequence
to have the maximal
possible period length ,
the polynomial
maps
onto itself and thus must be a permutation polynomial, which is either linear
() or
satisfies
according to [64, Cor. 7.5]. It turns out that the degree
plays an important role in the analytical examination of the generator in a
sense that a higher degree seems to indicate better distribution properties [70,
Theorems 8.2, 8.3] (see p. ). The theorem of Euler-Fermat tells us that evaluating
corresponds to the calculation of the multiplicative inverse. In this spirit, the
definition
of the EICG seems quite natural:
Definition 1.3 (Eichenauer-Herrmann [15]) Let
be a (large) prime and .
The explicit inversive congruential generator (abbreviated as “EICG”) with parameters
and
defines a sequence
in
by
and a sequence
of pseudorandom numbers in
by
As long as this generator
will always have period length .
Once again analytical and empirical investigations have shown that the output of this
generator is superior to that of an LCG. This will be the generator on which we will
focus our attention in this thesis. The other generators mainly serve as a reference
against which the EICG must compete.
1.3.5 EICG Variants
Two variations of the basic explicit inversive congruential generator
have been proposed. Both proposals substitute the prime modulus
with
. In the set
we can
define the modular inversion only for odd integers. This inversion is once again defined by
for all
odd .
Definition 1.4 (Eichenauer-Herrmann and Ickstadt [22]) Let
be a power of 2, and
with
and .
The explicit inversive congruential generator with power of two modulus with
parameters
and
defines a sequence
in
by
and a sequence
of pseudorandom numbers in
by
The conditions on
and guarantee that
the sequence is purely
periodic with period .
While powers of 2 as modulus have certain advantages for the implementation of
the generator, all theoretical investigations [22, 16] on the quality of the
resulting numbers have concluded that this generator is inferior to the original
EICG.
In order to achieve a period length of
,
Eichenauer-Herrmann [17] proposed the following generator:
Definition 1.5 Let
be a power of 2, and
with
and .
The modified explicit inversive congruential with parameters
and
defines a sequence
in
by
and a sequence
of pseudorandom numbers in
by
Although this modification does indeed increase the period length to
, the
theoretically derived properties of the resulting numbers are still inferior to the original
EICG.
1.3.6 Compound Techniques
An interesting meta-generator is the compound method. This is a very
simple and effective way to combine several streams of PRN into one single
sequence with (hopefully) superior properties. It works as follows: For
let
be a
purely periodic sequence of pseudorandom numbers. Then we get the compound sequence
by
If the subsequences are purely periodic with distinct period
, then we
have .
This compound method extends the well-known approach of Wichmann and Hill
[88]. The properties of the resulting sequence has been subject to a number of
publications; we refer to Niederreiter [72, 4.2] for all the references. Generally
speaking, the compound method preserves the basic properties of the underlying
generators.
Chapter 2
The Notion of “Randomness”
Examining what we mean by random numbers will help us to understand the
difficulties in generating pseudo-random numbers and interpreting test results. We will
look at how we all intuitively deal with supposedly random sequences, and touch upon
the mathematical treatment of the subject. Regrettably, we will not be able to
comprehensively cover this topic, thus we will focus on the subject of testing (finite)
sequences of PRN.
2.1 Randomness by Intuition
First of all, we want to take a closer look at the intuitive notion of randomness. For
one, we all intuitively assign probabilities to various events we encounter, from such
mundane things like which side a dropped slice of bread will land on, every-day events
like rainfall, the number of red traffic lights encountered, or friends met in the
bus, to explicitly random events like the outcome of a dice or the weekly
lottery.
But how do we come to the conclusion that one of these events is somehow random
? What are the criteria for that decision ? In some of the example above the decision is
easy as we know about the process which leads to the outcome. Watching the dice
being cast properly is a sure way to convince oneself that the outcome is
indeed truly random. But how do we proceed when we cannot look behind the
scenes, when the sequence of outcomes is the only information we have got
?
The human mind has remarkable capabilities to spot regularities in a sequence of
events. If it fails to notice anything suspicious it will declare the sequence to be
random.
Let’s test this notion on the most widely used source of random
numbers, the dice. A dice is supposed to select one of the numbers
in a fair and
independent fashion each time it is cast. In the following list we will argue on the merits of a few
possible outcomes.
-
{2}
- If we cast the dice just once, each of the possible outcomes are equally likely.
All sequences of length one are thus equally good.
-
{2, 4}
- There is nothing wrong with this sequence, too.
-
{6, 6}
- Casting doublets is not uncommon in the real world, thus they are not
reason enough to doubt the fairness of the dice.
-
{1, 2, 3}
- A sequence of length 3 is too short to arouse any suspicion, too. Such
simple patterns (runs up, runs down, only even numbers, only odd ones,
only primes, …) are actually quite likely to occur.
-
{1, 2, 3, 4, 5, 6, 1}
- With increasing length it is possible that a more clearly
visible pattern emerges within the numbers. Would you accept such a
sequence as generated by a real dice ? As these things still happen every
now and then in real life, the common answer to this question seems to be
“Yes, as long as this doesn’t happen too often.”.
-
{4, 2, 2, 2, 4, 2, 4}
- This sequence will give reason to doubt the fairness of the
dice. Whether the perceived skew is reason enough to outright reject the
sequence as random is a tricky question. After all, a real dice will show such
irregularities from time to time, too.
-
{6, 6, 6, 6, 6, 6, 6, 6}
- Although theoretical a possible outcome of a dice, this
sequence will probably not be accepted as such.
-
{6, 3, 2, 1, 2, 5, 4, 1, 6}
- At the first glance, this sequence looks quite random,
but closer scrutiny shows that it features alternately even and odd numbers.
As the probability for this to happen purely by chance is pretty small, one
gets suspicious about the “randomness” of the sequence.
-
{1,3,4,6,5,3,2,1,1,3,4,6,5,5,4,2,1}
- This one looks inconspicuous, too. But if
you draw the graph of the sequence you will notice a regularity: There are
too many long ascending or descending subsequences. As these long “runs”
should not appear that frequently in random sequences, this one does not
seem to be random.
-
{1,2,5,4,3,6,6,2,4,1,3,5,5,2,3,4,1,6}
- What about this sequence ? Can you
see any regularity in it ? Once again, a casual look will not find
anything suspicious, the distribution of the numbers seems to be balanced,
consecutive numbers do not have any special relation and there is nothing
wrong with the runs, too. Actually, the numbers are balanced way too
good as all six numbers appear before the first one gets repeated. In
other words, the sequence consists of three permutations of {1, …, 6}. If
the equidistribution of the numbers is so perfect, the randomness of the
sequence must be challenged.
-
{3,2,5,2,1,4,4,6,2,3,4,5,2,5,6,3,3,1,5,4}
- This sequence has a hidden regularity,
too. In previous sequences we have looked for correlations between consecutive
numbers. If we generalize this and take a closer look at numbers
steps apart, we have a more versatile tool for finding regularities. It turns out
that
holds for all values of .
Such a “long range” correlation should not happen in random sequences.
Did you see the one big fault in this sequence of would-be random sequences ? We did
not notice it because we looked only at single sequences. Can you find it now
?
Let us summarize the arguments:
- If the sequence has properties we do not expect to be present in random
numbers, we get suspicious.
If we argue about the “randomness” of a given sequence we try to find
reasons for rejecting it as random. There seems to be no way of asserting a
sequence to be random, it is only the absence of arguments to the contrary
that will lead to confidence in the sequence. The proper formulation in
the language of statistics is the following: The null hypothesis is always to
assume the sequence was indeed generated by a random process with well
known statistical properties. As we will see later, it is not possible to reverse
the problem and regard the non-randomness as the null hypothesis.
- Longer sequences are easier to judge.
Short sequences are likely to contain some sort of perceived regularity, thus
it is hard to reject such a sequence based on a suspicious pattern. If the
sequence is long enough to check if the pattern continues to appear in it,
one can try to determine if the pattern is part of some systematic fault or
just coincidence.
- There are a lot of ways a sequence can be suspicious.
Just when we thought we have found a sequence which does not exhibit
the patterns we have found in all the previous faulty ones, it turns out that
there is a different kind of regularity in it. Somehow this is just like the trick
question for the first natural number without any special properties. If such
a number existed, the very fact would make it special, thus there can be no
such number. We almost get the same feeling when we examine sequences
for their non-conspicuousness. As there are so many ways a sequence can
exhibit a pattern, a complete absence of patterns is just as conspicuous as
any weak regularity.
Furthermore, it is worth pondering if there are not so many patterns that
all sequences will exhibit one. We will take a closer mathematical look at
this question later.
- “Perfect randomness” is an oxymoron.
If the “random” sequence exhibits exactly the expected distribution this
will cause suspicion, too. A random sequence is supposed to deviate from
its distribution. The common measure for this is the variation. A sequence
with a perfect distribution will fail to have the same variation a random
sequence is supposed to have.
As the variation can be viewed as just another test statistic, it, too, should
vary in a certain way. From that point of view, a constant and perfect
variation is just as suspicious as a constant and perfect distribution. This
reasoning leads to the demand that not only the distribution of the numbers
should be as wanted, but also that the empirical higher moments should be
close to the values predicted by probability theory.
2.2 Formalizing the Intuitive Notion
Now that we have examined what we intuitively mean by saying “This sequence looks
random.” we can try to formalize this notion and develop a set of properties we want
to check if we have to judge a sequence and its generating algorithm. The goal in this
formalisation is to be able to delegate the testing to computer programs. As computers
are known to be very bad at spotting patterns, it will not be an easy undertaking to
find an algorithm which does as good as the human mind. We can only hope that all
systematic faults in the sequence will eventually cause a suspicious behaviour of the
sequence in a generic test.
In the following we abandon the dice as the example, and turn to uniformly distributed numbers
in the interval .
-
Distribution:
-
The first step in testing a sequence is usually to test its distribution characteristics.
That is, are the numbers equally spread over
?
In order to test the (empirical) distribution one partitions the interval
in sets
and compares the number of hits in each set to the size (measure) of that
interval.
In the discrete case this can be done by simply counting how often each
possible value appears in the sequence. If the counts differ significantly, the
distribution property of the sequence is inadequate.
In order to keep the problem manageable in the case of a huge number of
possible outcomes and in the continuous case, the bins (i.e. the )
used for counting will cover more than one outcome.
The layout of the partition is a crucial part of the test: If the
are simple intervals the test will measure the overall distribution of the
sequence. But the
could be the union of a set of small intervals, in which case the test targets
irregularities in the fine structure of the sequence.
Once we have finished the counting process we need some mathematically
justified criteria for interpreting the difference between the number of hits in
each
and the expected count. There are a number of possible algorithms for this,
the most popular of which are the -test
and the Kolmogorov-Smirnov test (often abbreviated as KS-test). The former
uses a test statistic based on the difference between expected and actual
count in each bin, whereas the latter compares the empirical distribution
function of the counts to the expected one.
-
Correlations:
-
It should be clear that any numbers in a deterministically generated and
thus reproducible sequence are trivially correlated. Therefore it makes no
sense to look for such intricate dependencies like the generation rule in the
sequence. We will restrict our search to much simpler correlations, which
makes additional sense because that will be the only kind of correlations
we can hope to find with the limited capabilities of a computer program.
There are two approaches to this:
Tests for special correlations check if the sequence exhibits a given kind
of regularity. An often used example is the run-test which measures
the frequency of ascending or decreasing parts in the sequences. The
distribution of these runs in random sequences is known, making it possible
to judge the sequence with respect to this type of correlation.
The serial test is a more general way of examining a sequence. It transforms
the problem of testing for correlation to the problem of testing for equidistribution
by looking at tuples composed of elements from the sequence. The size of
each tuple is called the dimension
of the test. Common tests use either overlapping tuples defined as ,
or non-overlapping tuples defined as .
If there are no correlations in the original sequence the -tuples
are equidistributed in the unit cube of dimension ,
which can be checked using the techniques outlined above.
To illustrate this, let us examine the sequence
with the serial test of dimension 2.
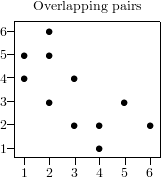
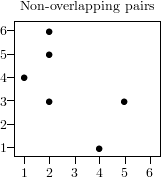
As you can see, the fact that large and small numbers alternate causes a
significant deviation from the equidistribution of the points.
For a number of generators it is possible to derive analytical
bounds for the deviation from the equidistribution of
-dimensional
tuples as measured by the discrepancy.
If one does not restrict oneself to form tuples out of consecutive numbers, the resulting test
will be able to find more subtle kinds of correlations without resorting to high dimensions
.
While this modification hardly changes the empirical testing, only in the case of
the EICG analytical bounds have been derived for this generalized serial
test.
2.3 Randomness in Mathematical Terms
Now that we have clarified the intuitive understanding of the concept of testing
pseudorandom sequences, we will turn to the mathematical treatment of the subject.
Rather than providing a full scale discussion of the mathematical objects and
formalisms involved, which would exceed the scope of this thesis, we want to present
an introduction targeted at the mathematical layman. Our aim in this section is to
introduce as much of relevant concepts as is necessary to be able to explain the
problems one faces when testing pseudorandom numbers and comparing PRNG. We
refer to [85] for an in-depth discussion.
There is more than one mathematical approach to this topic. The following list
tries to introduce the different viewpoints and gives references for further
reading.
- Number-theoretic approach.
In our context, this branch of mathematics focuses on the equidistribution
of a sequence of numbers.
Various measures for the quality of the equidistribution were developed over
the years, of all these numbers, the discrepancy is the most common.
Theorems on the equidistribution usually deal with infinite sequences, thus
they are not particularly useful in conjecture with finite (or periodic)
sequences. For example, equidistribution of a sequence can be defined in
terms of the discrepancy in the following way:
See [51, 70, 72] for further reading.
- Kolmogorov complexity and information theory.
This approach targets the complexity and information content of the
sequence in question. One of the possible measurements is the minimal
size of a computer a program (or a Turing machine) which can reproduce
the sequence. In the optimal case, the program code will have to explicitly
contain the sequence in order to print it. Any possible shortcuts the program
can use (like exploiting dependencies) will be a measure for the lack of
randomness of the sequence.
Since all our sequences are generated by short programs, they a-priori fail
this test. Thus we will not consider this notion in our tests.
A similar approach is to focus on the amount of information contained in
the sequence. If the entropy is high enough, we will accept the sequence
as a good approximation of random numbers. Another way to express this
notion is to state that the sequence is not compressible.
Testing whether a sequence is compressible is not easy since all common
implementations cannot achieve the theoretically possible compression.
Only really bad PRN can be eliminated with programs like gzip or
compress. Extending the capabilities of these programs (for example
enlarging the range of the pattern search in gzip) might be a way to get a
workable test. As far as we know, nobody has tried this yet.
For larger sequences, the distinction between these ideas start to blur, as
the size of the information needed to transform one representation into the
other becomes irrelevant.
See Lagarias [52], Ming/Vitány [67] and Chaitin [5].
- Cryptographic considerations.
A sequence of PRN can be used to construct a stream cipher. If “true
random” numbers are used, this cipher is called the one-time pad and is
provably secure. So it is natural to ask what properties the PRN must have
to achieve a good level of security.
According to Rueppel [76] there are several approaches to the construction
of a secure stream cipher: The information-theoretic approach considers the
possibility in principle to derive the seed (i.e. the key) from an observation of
the PRN, the system-theoretic approach tries to make breaking the cipher at
least as hard as solving known “hard” problems like factoring or the discrete
logarithm. The complexity-theoretic approach tries to make sure that the
amount of work needed to break the cipher is of non-polynomial complexity,
randomized stream ciphers increase the magnitude of the code-breaker’s
problem by utilizing a public pool of random numbers.
See [77, 76] for a discussion of these ideas.
- Statistical approach.
The basic idea of statistical testing can be summarized as follows: From
a sample of supposedly random numbers a function called test statistic is
calculated. As the distribution of this function is known for the case of
real random numbers (otherwise the test does not make sense), one can
determine which kind of results are extremely unlikely to occur. Typically
this is formulated as intervals in the domain of the test statistic. These
intervals (usually called critical region) are selected in a way that the
probability that real random numbers lead to a test statistic there is smaller
than the level of significance (usually 0.05, 0.01 or 0.005). If now for a
sample of PRNG the test statistic falls into the critical region the common
inference is to reject the sample.
See [50, 4, 54] for further reading.
All common tests rely on the idea of statistical testing. In the following we will try
to elaborate on the motivation behind these tests, their mathematical foundation, their
power and limitations, and how to interpret their results.
2.3.1 Random Variables and Probability
First of all, let us take a closer look at what we want to simulate. Our target are
sequences of random numbers, which are realisations of a sequence of independent,
uniformly distributed random variables.
Random variables (RVs) are one of the main building blocks in probability theory.
They are used to assign each possible outcome (or, to be more exact, each reasonable
set of outcomes) of an experiment a real number which is interpreted as the probability
of this outcome.
But strictly speaking, the mathematical concept of RVs does not explicitly reflect
our intuitive ideas about randomness of events, on the contrary: RVs are just simple,
ordinary functions. One is tempted to ascribe mythical powers to RVs, like the ability
to randomly select one of a set of possible events. This is not true, they only
describe certain aspects of an idealized system which flips the metaphorical
coin.
So where is the link between the mathematical world of RVs and the real
life world of roulette tables ? Unfortunately there is none for single events.
Even if a RV does in fact model a real world event, hardly any conclusions
can be made about the outcome of the next single event. Even such unlikely
events as winning the jackpot in a lottery do happen every now and then,
and most people are not deterred by the extremely bad odds from playing
every week. On the other hand some people are scared of travelling by plane
because the probability of a safe flight is marginally less than one. In both cases
our experience tells us that the probability alone cannot predict the next
outcome.
But even such pretty definite sounding statements like “this event
will occur with probability 1” cannot guarantee the outcome of an event.
More insight into measure theory will tell us why such strange things
can happen. For example, the probability that the next realisation of an
-distributed
random variable will be a rational number is zero. This does not stop the real
world from delivering one of the infinite number of rational numbers, thus
rendering the statement “This experiment will only return irrational numbers”
incorrect.
We have seen that a RV cannot make concrete statements about a single
outcome, so we might ask what statements about outcomes it can make at all.
One way to formulate the meaning of probability is the following: [85, p.
10]
The probability assigned to an event expresses the expected average
rate of occurrences of the event in an unlinked sequence of
experiments.
We need to elaborate on two aspects of this definition as they are not as strict and
unambiguous as commonly demanded from a good definition.
First, what do we mean by “expected” ? That seems to indicate that
probability cannot be an intrinsic property on an event. There is no
mathematically satisfying way to assign a probability to an event based on a
(finite)
set of measurements, as it is extremely unlikely that another set of experiments will
result in the same value. The common way out is to make assumptions about some
parts of the experiment, like the Laplace assumption which assigns the same
probability to all underlying events. These assumptions are based on a mental model
of that event which includes a theory on how often something should occur. It is the
mathematician, the physicist or just some observer who forms a mental model based
on experiences or consideration. Such simplifying mental models of the real world are
ubiquitous as they provide an essential simplification in the way we view the world.
Other such simplifications include the concept of rigid bodies, fluids, or gases which
are abstractions of “a bunch of molecules tied together by various forces”. Just as the
laws of leverage rely in their formulation on the concept of forces and of rigid
bodies the laws of chance depend on the concept of probability assigned to
events.
The other critical word in the above definition is “unlinked”. By unliked we mean
that the outcome of one experiment does not influence the outcome of any subsequent
experiment. Common examples for unlinked experiments include drawing balls
from an urn (with putting them back in !), casting a dice, or the roulette
wheel. Please note that in all these examples there is a connection between
two successive experiments as the first one does influences the second. It is a
conscious decision by the observer that the re-shuffling of the balls in the urn
caused by the first experiment does not affect the probability in the second one.
This sounds almost like a paradox, as the re-shuffling surely does effect the
outcome. But remember, just above we noted that the probability of an event
does not determine the next outcome at all, so there is not contradiction
here.
We have to be careful with sequences of PRN and their relation to independent
random variables, too. The concept of independence is based on the concept
of distributions. As we cannot ascribe distributions to numbers, we cannot
use the term “independence” for sequences of PRN. We will use the word
correlations to refer to any unwanted relationship between elements in the
sequence.
2.3.2 Testing
As described above, the theory of random variables and probability tries to model
aspects of the physical world. The fundamental principles of science demand
justification in form of experiments for all such theories. For typical physical models
such experiments are usually easy to set up and follow the same scheme of comparing
an expected (calculated) result to the measurements of the actual physical event. If
they differ more than inaccuracies in the measurements would allow, the theory is
proven to be wrong. Philosophy of Science tells us that it is impossible to positively
prove a theory.
Do the same principles hold for conjectures in the field of probability, too ?
Unfortunately, they do not. Let us illustrate this with an example:
As a theory to test we might take the assumption that a given coin
is fair, meaning that the probability it lands with the heads side up is
. How
might an experiment designed to test this hypothesis look like ? Surely it will involve
throwing the coin a number of times and then comparing the result to the prediction.
Calculating the prediction based on the theory is simple, unfortunately the
prediction assigns each possible outcome a positive probability. Thus regardless
of the behaviour of the coin the result is consistent with the theory, as we
cannot rule out the measured result. If we have no way to reject a theory,
we have to find a different set of criteria according to which we can justify
theories.
The common way out is statistical testing. It should be clear that statistical
testing can never be as strict as testing in other areas. It is a heuristic approach to the
problem. As such, it relies on the good judgement of the tester and is not
objective. But before we elaborate on the shortcomings of statistical testing let us
summarize the basic procedure again, already using the test for randomness as the
example.
- The first step is to formulate the hypotheses. In our case the null hypothesis
states that the source of our pseudorandom numbers can be modeled as a
RV with distribution .
The alternative hypothesis
states that
is not true.
- We define a function called test statistic which maps the result of an
experiment into some mathematical domain. Typical test statistics for testing
uniform PRN are the number of runs, the discrepancy, the -statistic,
…. See [50, 54, 70, 66] for further test statistics.
- A level of significance
is selected which defines how strict the test will be and how much leeway we
will accept for the PRN. Common values for
are
or .
- Using the (hopefully) known distribution of the test statistic for the case of
being true, we determine the critical region
which is the area in the domain of the test statistic which covers its extreme,
unlikely values. The value for
is used to quantify what we mean by “extreme” and “unlikely” in such a way
that .
- Now the pseudorandom numbers are generated and are used to to calculate
the test statistic. If the value for the test statistic falls into
we say that the PRN have failed the test and we have reason to believe that
is true, otherwise the test is passed and we have no reason to reject .
This is the basic outline of all common empirical tests. We will discuss a few tests
and their results later in this thesis. So what are the weak spots in this method of
testing pseudorandom numbers ?
- PRN are not experiments.
First of all, when testing sequences of numbers generated by a PRNG basic
premises of statistical testing are violated.
The theory behind statistical testing assumes that we actually deal with
random events. It is thus a circular argument to conclude from the result
of such a test that the numbers in question are “random”. Only their
statistical properties that are subject to the test, not the basic premise that
the concept of random variables is a valid model for that experiment.
It is therefore not correct to speak of “statistical testing” with respect to
PRN testing. A more appropriate term is “numerical testing” as the
test examines only a numerical property of a fixed set of numbers.
The only “statistical” part of the test is the calculation what numerical
values for the test statistic are considered to be good and which are
considered to be bad.
- The test statistic is arbitrary.
The test statistic determines which aspect of the numbers we want to test.
Dividing
into the intervals
for ,
counting the hits in each interval, and then calculating the
statistic is a straight-forward test statistic which aims the the overall equidistribution
of the pseudorandom numbers in .
The choice of the bins (in this case intervals) seems to be a natural one.
But what bins should we use to measure the finer aspects of equidistribution ?
We could use just a large value for
and keep the intervals, but that would cause a problem with the validity of
the
approximation as the number of hits per bins decreases. An other option is
to use something like this: Define bin
as
for some suitable values for
and .
Then the bins are no longer simple intervals, but sets of intervals that are
spread over the unity interval. The value for
determines the width of each component interval.
Is there a natural choice for
? We do not think so. But the choice can be important as the result of
the test depends on it. Consider for example the set of numbers defined by
which is perfectly equidistributed in.
For certain relations between ,
and ,
like ,
the test will result in extremely bad
statistics. As an example, consider the case
where all numbers
fall into the same bin. For other values of ,
this set of PRN will exhibit no weakness in this test.
We have seen that even such simple changes to the test statistic, like
modifying the width of stripes, can completely change the result of the test.
One can imagine that completely different layouts of bins will lead to a
great variance in the test results, too. Thus we have to keep in mind that
the choice of the test statistic, and thus to some extent the result of the
test, is arbitrary.
One consequence of this fact is that we cannot declare one sequence of
PRN to be better than a second one just because we found a test where
the first one rates better, as a slightly modified test might produce exactly
the opposite result.
- Good PRN have to fail some tests.
What we strive for are numbers who behave in most respects like realisations
of -distributed
RVs, so it is a natural question how such ideal random numbers will perform
in our statistical test. The answer to this is quite simple: If we conduct a test
at the significance level
then a sequence of random numbers will fail the test with probability
.
If we have set
then we can expect a failure about once every hundred tries.
As PRN should model all aspects of real random numbers, they should fail
statistical tests at about the same rate.
It is therefore not advisable to outright reject a sequence of
PRN based on its failure in single tests.
- The variance of the test statistic can be important, too.
Classic statistical tests examine if the test statistic does not deviate from its
expected value too much. If we are only interested in the expected outcome of a
similar simulation problem, such one-level statistical tests are all we need in
order to be confident about the accuracy of the simulation.
On the other hand we might be interested in the distribution of the simulation’s
outcome. For this goal hitting the expected value is not enough, the variance of
the result is now important, too. Thus we will demand the same behaviour from
the test statistic, too.
Let us illustrate this principle with an example. We want to test the well known
strategy of doubling the ante in a game of roulette. It is supposed to guarantee
winning the initial ante and works like this: If we do not win in the
first round (and therefore win twice the ante) the ante is doubled for
the next round. If this round is won, we get back four times the initial
ante while we invested three times the initial ante resulting in a net
win of one ante. In case of bad luck we double the ante again hoping
for eight times the ante for an investment of seven. As we hope that
we will finally win before our capital is drained a net win seems to be
certain.
In order to simulate this we need random numbers to determine
whether we will win the current bet. The probabilities are
for winning
and
for losing each round, respectively. It seems to be natural to use the lengths
of runs as a test statistic to test our source of PRN for its fitness to
simulate a real roulette table. The probability that the maximal run
length in 500 tries is greater than 15, is smaller than all usual values for
, so
according to the corresponding statistical test we should reject all sequences where such runs
do occur.
When we now run the simulation with these prescreened sequences we will never
ever experience a loss as long as we have enough money for 15 steps of
doubling the ante. Thus we should conclude that the strategy works. As
we know, this is not true. So what went wrong with our simulation
?
The statistical test considered it equally important whether the
sequence in question was “well-behaved” or not, whereas the
simulation assigned completely different weights to those cases. Thus
the area that the test considered to be insignificant (smaller than
)
played a major role in the simulation (more than
).
There are some other cases of simulations where we are not so much
interested in the average case, but in the extreme ones. Consider for example
all those safety measures in power plants or other machinery where a
rare sequence of occurrences might lead to catastrophic results. When
simulating these security systems one must not a priori exclude unusual
sequences.
Please note that the distinction between level-1 and level-2 tests (tests which test
the distribution of the results of a level-1 test) is arbitrary. The test statistic of
a level-2 test is just another function of the underlying set of PRN,
too.
- Statistical tests cannot be used to objectively rate PRN.
One might be tempted to use a set of statistical test to once and for all declare
one generator superior to another generator. Intuitively this makes sense,
especially when comparing two generators of the same type. A common use for
this heuristic is the selection of optimal parameters for the LCG based on its
lattice structure [29, 73].
But is this judgement mathematically justified ? Leeb explains in [59] that such
judgement is not justified as all possible sequences of PRN of a given finite
length pass exactly the same number of statistical tests.
In order be able to use statistical tests as a criteria for the selection of
PRNG the user has to declare which properties he considers important. With
this knowledge it is possible to weight the tests and therefore select a suitable
generator for this specific application.
- Statistical tests are simulations with a known result.
Both statistical tests and simulations use a set of PRN to perform a more or less
elaborate calculation.
In a statistical test we draw a conclusion from the right side to left: Based on
the difference between expected and calculated value we judge the quality of the
PRN.
A simulation operates the other way round. Based on the (hopefully) known
quality of the PRN we hope that the simulation result is correct.
While generic statistical tests can be used for this reasoning, one can increase
their value by designing the tests to closely model the simulation. Thus the tests
can target exactly those properties in the PRN which will be significant in their
application.
2.3.3 Interpreting Test Results
In order to conclude this chapter on the notion of randomness let us recapitulate what
we know about testing a generator, and how we should proceed when we face the task
of selecting a generator for a particular simulation problem.
- Statistical testing cannot guarantee that the tested generator will perform
equally well in a real world simulation. Only if we are able to determine
which aspects of randomness are important for the simulation and
specifically test our source of pseudorandom numbers for these aspects, we
can mathematically justify our confidence in the validity of the simulation
[59].
- Empirical testing should be supplemented by analytical investigations
into the quality of the generator. Such calculations are often essential to
guarantee basic properties like period length, as well as to provide means
to select suitable parameters to avoid pitfalls like a degenerated lattice in
the case of linear generators.
Furthermore, analytical investigations can yield some insight in the overall
structure of a generator’s output which can be compared to the properties
required in the simulation. The lattice structure of the LCG might be
actually useful in Quasi-Monte Carlo integration whereas it can be harmful
in geometric problems, e.g. the nearest-pair test [14, 54].
- Level-one tests target only the expected value of the test statistic. Often
this is not enough, making it necessary to test the distribution of the test
statistic. Such two-level tests guarantee that the proper irregularities are
present in the PRN, too. Whether we should strive for such variance in the
generator is up to its final application.
- Rejecting a generator is rejecting one facet of randomness. It is
self-deception to claim that one rejects a generator based on its lack of
randomness. One can only state that one does not want that particular
aspect of randomness. Sequences we will intuitively classify as non-random
may be important as input for the simulation in order to get correct results.
- As we have seen before, the results of a test can be extremely sensitive to its
parameters. Thus statements like “generator x passes the y-test” have little
relevance unless the exact parameters used in the test and in the generator
are published, too.
- The result of a single test is not enough to assess the quality of generator.
Only a battery of tests and comparisons to the performance of other
generators in the same test suite enable the mathematician to pass
judgement on a generator.
Chapter 3
Theoretical Results
In this chapter we will discuss analytically derived properties of the explicit inversive
congruential generator (EICG). We will use results obtained for the LCG to serve as a
reference as the LCG is the most commonly used generator. Let us start by repeating
the definition of the EICG:
Let be a (large)
prime and .
The explicit inversive congruential generator (abbreviated as “EICG”) with
parameters
and defines
a sequence
in by
|
| (3.1) |
and a sequence of
pseudorandom numbers in
by
Please remember that we perform all calculations except the final scaling in the finite
field .
will denote the
non-zero elements of ,
that is . The over-line
denotes the multiplicative
inversion in for all
non-zero elements .
With the special case
added, is a bijective
function from
onto . Furthermore,
we have
and for
all .
The latter identity is due to Fermat’s Little Theorem.
Note that from the explicit definition of the sequence
we
can easily derive a recursive description:
In order to achieve maximal period length
, the parameters
,,
and can be freely
chosen from as long
as is prime and
. To see this, consider the
function which is composed
of bijective functions in and
thus is bijective, too. As
in we have
for all
, thus the sequence
is purely periodic
with period length .
We will only consider full period generators, that is
.
We will write
to denote the output of a particular instance of the EICG method. Unlike Leeb [59, p.
89] we mean the whole infinite (but periodic) sequence, and not just the first
numbers. This way, no special treatment of wrap-arounds is needed when considering
subsequences.
3.1 Relations between different EICG
The choice of parameters is simple for an EICG, but not all choices will lead to
completely different pseudorandom numbers. In this section we will examine the
relations between EICGs with the same modulus, but different parameters
,
, and
.
These results are helpful for the implementation, as one can eliminate an addition
modulo ,
as well as to the theoretical investigation as they provide a very elegant way to
describe sub-streams. We will elaborate on this idea which is due to Niederreiter [71, p.
5] later on.
First of all, let us make a rather trivial observation on the role of the parameter
.
Observation 3.1 Let .
Then we can write the sequence
as .
In other words, the second sequence is first one shifted by .
Proof: This relation follows from the fact that
and
appear only
as their sum
in the definition of the EICG. __
The following observation is taken from Leeb [59, p. 89]; it states that one of the
parameters is redundant.
Observation 3.2 Let
be prime and be fixed.
Then we have for all
and
|
| (3.5) |
Proof: We base the proof on the recursive definition of the EICG. As the recursion does only
depend on ,
which is constant, it is sufficient to show that the
of
these generators are equal. In the first two cases we have
and the third equality translates to
_
The third equality can be used to rewrite any EICG as an EICG with
, but a different
value for .
Thus the generating formula can always be rewritten as
which saves one addition. The addition
can be implemented by simply incrementing the previous value modulo
, thus
we need to perform only one increment, one multiplication, one inversion, and one
division to generate the next pseudorandom number.
There is an obvious connection between
and
,
too:
Observation 3.3 Let
be prime, ,
and .
The sequence
can be obtained by selecting every -th
element from the sequence .
Proof: The sequence generated by taking every
-th element in the
sequence can
be written as .
We have
and thus
where .
_
These three observations give us the tools to show that all
maximal period EICGs can be derived from the “mother-EICG”
in the
following way:
- Start with the sequence .
- Shift the sequence by .
The result is .
- Take every th
element of that sequence. According to Observation 3.3 we get .
- According to Observation 3.2 this sequence is the same as .
Can these insights help us in the theoretical investigation on how samples from
an EICG behave under various tests ? Yes, they provide a very convenient
and elegant formalism to describe subsequences and various kinds of
-tuples
generated from the stream of pseudorandom numbers. With this formalism, the proofs
of discrepancy estimates and non-linear properties are very concise.
First of all, we do not need to bother with the parameter
in
the theoretical investigation as we can always rewrite the EICG to one with
.
Second, any property of a sequence of EICG numbers, which is valid independently
of the parameters used, is immediately valid for subsequences consisting of every
-th
element. One direct consequence of this is, that once we can prove that pairs of
consecutive numbers are uncorrelated for all valid parameters, we can rule out the
possibility of long-range correlations at critical distances. See [10, 20] for a discussion
of such problems inherent to the LCG.
The third gain, due to Niederreiter [71], is to be able to write almost arbitrary
-tuples
formed out of the stream of EICG numbers as parallel streams. Such
-tuples
as usually used to examine the correlation between successive numbers. For example,
the overlapping serial test (see page ) tests the equidistribution of the vectors
|
| (3.6) |
for in order to
test the PRN
for correlations. If we pick the first coordinate of each vector we get the original sequence.
Picking always the second results in the original sequence shifted by one. According to
the above equivalences we can write this shifted sequence as an EICG with the same
parameter ,
, and a
different .
Thus we have
|
| (3.7) |
where is the sequence
generated by the EICG .
The obvious generalisation is to allow almost arbitrary
EICGs
for each coordinate.
In the following, we will prove all statements on the behaviour of
-tuples in
terms of these parallel streams. For that, we will need to restrict the possible values for
the and
in order to avoid certain
special cases like .
As we will see later in the various proofs, we need the condition
for all
. Thus
we have the following definition:
Definition 3.1 (Parallel Streams) Let
be prime,
, and
,
such
that
are distinct. Then we put
|
| (3.8) |
and define a sequence
in the -dimensional
affine space over
by putting
An interesting special case of parallel streams, which is more general than the overlapping
-tuples
considered above, can be obtained as follows. Choose an integer
with
and
integers
and put
where the are as in (3.1).
This sequence of points in
can be written in terms of parallel streams according to Definition 3.1 by putting
and
for
. It is easy to
show that the
are distinct, thus all results concerning parallel streams are valid for this general method of
composing -tuples,
too.
The non-overlapping tuples
are covered by the concept of parallel streams, too. To see this, set
and
for
.
3.2 Structural Properties
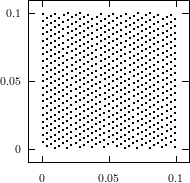
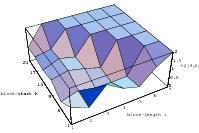
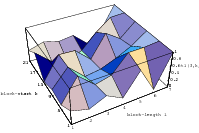
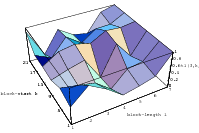
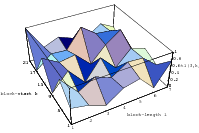
The best known structural property of any pseudorandom number generator is the lattice
structure of the LCG. Coveyou/MacPherson [9] and Marsaglia [65] noted first that
-tuples
formed from successive LCG-numbers form a lattice in the
-dimensional
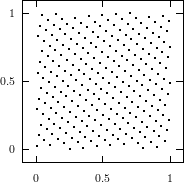
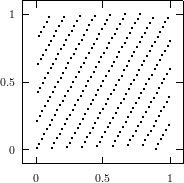
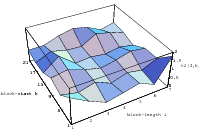
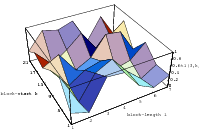
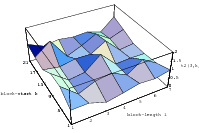
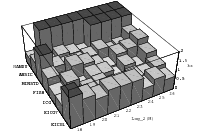
cube. Figure 3.1 depicts the lattice formed by plotting overlapping 2-tuples
for the full period of two “toy” generators. “Production quality” generators
exhibit the same structure, you just have to zoom into the image to see the
pattern.
The shape of the lattice depends very strongly on the parameters
and
of the
LCG. Thus various measurements on the coarseness of the lattice are used to select suitable
parameters
and .
That way, a weakness of the LCG turns into a strength, as one can guarantee a
well-behaved lattice for low dimensions as long as the parameters are chosen well
enough.
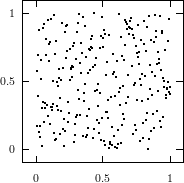
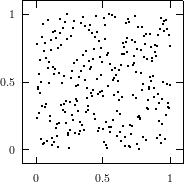
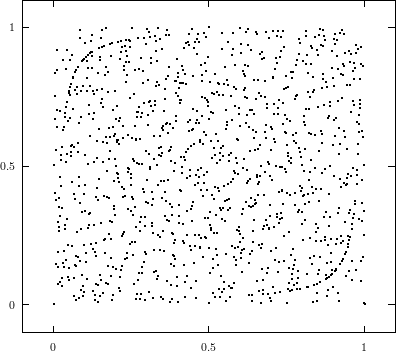
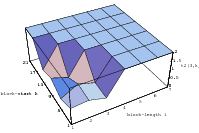
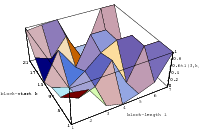
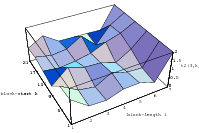
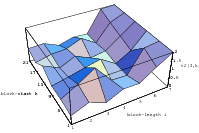
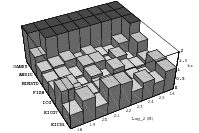
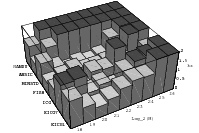
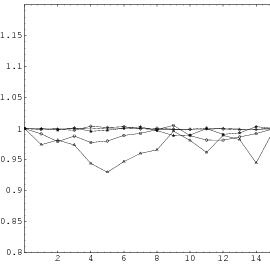
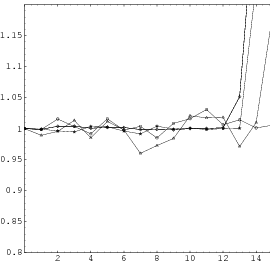
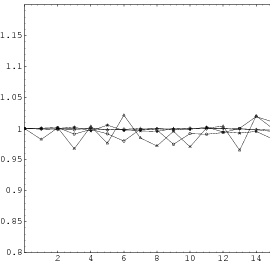
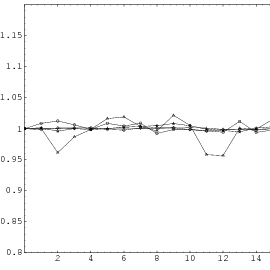
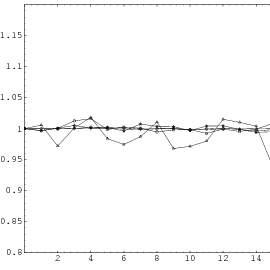
Does the EICG exhibit a similar structure ? Figure 3.2 suggests that the
EICG does not possess this linear property, although one can see some other
regularities. In fact, one can prove a very stringent non-linearity property for
-tuples
taken from an EICG. The theorem describing this is due to Niederreiter [71].
Theorem 3.1 Let
as in Definition 3.1, then every hyperplane in
contains at most
of the points ,
,
with .
If the hyperplane passes through the origin of ,
then it contains at most
of these points .
Proof: All calculations in this proof are performed in the finite field
.
Furthermore, remember that according to Definition 3.1, the
are
distinct.
A hyperplane
in is uniquely
defined by a vector
and a scalar as
. We restrict our search for
points on a hyperplane .
Thus for we have
according to (3.8) ,
therefore we can rewrite the hyperplane equation for
as
By clearing denominators, we see that
is a root of the polynomial
If ,
then is a
nonzero polynomial
of degree over
. Since such a
polynomial has at most
roots in , the
hyperplane
contains at most
of the
with .
If ,
that is ,
we get
whose degree is at most .
It remains to show that is
not the zero polynomial. As
is not the zero vector, one of its coordinates is nonzero. For
we
have
because is the chosen
nonzero coordinate, and the
as well as the
are nonzero according to the conditions of the theorem. As we have found
for
some ,
cannot be the zero polynomial. __
This theorem proves that -tuples
taken from an EICG do not form any linear structure such as a lattice. But that
does not mean that no other kind of pattern emerges in plots of pairs of
consecutive
numbers. For example, consider Figure 3.3, where one can see a hyperbola-like
structure in the upper left and lower right corner. Eichenauer-Herrmann and
Wegenkittl are currently preparing a paper discussing these properties of the
EICG.
All the plots so far contained all the overlapping pairs available from the full
period of the generator. This way, the underlying structure of the generator
is perfectly visible. But usually one does not utilize the full period of any
generator; a common rule of thumb is to use not more than the square root of the
period. Thus the LCG will never be able to build up the full lattice and the
EICG will contain only a few points on hyperbola. Figure 3.4 depicts the lattice of
lcg(65536,325,1,1), the first image shows the full lattice in a zoomed view, the second
one contains only 256 points, which corresponds to the square root of all possible
points.
These figures clearly demonstrate that any regularities a generator develops over
the full period are not necessarily present when only a fraction of the available
numbers is used. The recommendation never to exhaust the full period can be further
justified by the following argument: The PRNG is supposed to simulates drawing
numbers from an urn with putting the numbers back into the urn, but in fact the
typical PRNG empties the imaginary urn before it puts all numbers back when the
period is exhausted. The difference between “drawing with replacement” and “drawing
without replacement” is small as long as only a fraction of all numbers are drawn from
the urn.
3.3 Correlation Analysis
The discrepancy is a widely used and well studied measure for the equidistribution of a
set of points. In this section we will try to give a motivated definition, some
theoretical background, and summarize all published results concerning the
EICG.
3.3.1 Background
There are at least three approaches to the notion of discrepancy, one stems from
statistics, one from geometric reasoning, and one from numerical integration. We will
use the latter. An extensive introduction to discrepancy can be found in Niederreiter
[70, Chapter 2].
We will use the following setting: The closed
-dimensional
unit cube
will be the integration domain in which we will try to integrate the function
by
using the quasi-Monte Carlo integration
|
| (3.9) |
with .
Ideally, we hope that the approximation converges to the integral as the number of points
increases. If this is the case for a reasonable class of functions, say, for all continuous
on
, then we call the
(infinite) sequence
uniformly distributed in .
One can show that this definition of “uniformly distributed” is quite independent of
the class of functions; using the Riemann-integrable functions yields the same test as
using the characteristic functions of a very simple set of intervals.
Whereas the limit of the integration error can be used as a qualitative measure for the
distribution properties of an (infinite) sequence of points, one can use the integration error
in the finite case as a quantitative measurement of the equidistribution of the finite sequence
.
In order to get a workable measurement, we have to state which family of functions
we
consider for the integration, and how we condense all the integration-errors for each
function from the family into one single number.
The general concept of discrepancy uses the set of characteristic functions of axis-parallel
cubes in
as the functions to integrate and the supremum as the condensing function. Formally,
we can write this in the following way:
If is a finite
sequence in , and
an arbitrary
subset of ,
then we can express the quasi-Monte Carlo integration of the characteristic
function
in terms of the
number of
in ,
as
Based on this, the error when integrating
can be
written as ,
where is the
-dimensional
volume
of .
Thus we can write the general notion of the discrepancy of a finite sequence
of points
in for an
arbitrary
family of
sets as
|
| (3.10) |
From this general definition we can derive the definition of the two most important
incarnations of discrepancy as follows:
Definition 3.2 The star discrepancy
of the finite sequence
is defined by ,
where
is the family of all subintervals of of
the form .
Definition 3.3 The (extreme) discrepancy
of the finite sequence
is defined by ,
where
is the family of all subintervals of of
the form .
While
and
are the classical figures for measuring the equidistribution, they are far from being the
only ones. Interesting variations of the basic idea are the isotropic discrepancy,
which uses the family of convex sets instead of axis-parallel cubes, or the
-discrepancy, which uses the
-norm instead of the supremum.
Especially the -discrepancy
has received a lot of attention recently as it is suitable for empirical testing [38] and
has a number of interesting theoretical properties [80, 62]. Another measurement
worth mentioning is the weighted spectral test [40, 46, 44, 41, 47].
Let us quickly state a few general results concerning discrepancy. They will help us
to interpret the main results of this chapter. We once again refer to Niederreiter [70, p.
14ff, p. 166ff] for proofs and further references.
Proposition 3.1 For all finite sequences
consisting of
points in
we have
and
In dimension one, that is ,
it is possible to express the discrepancy as a relatively simple formula operating on the
ordered list of points.
Proposition 3.2 If ,
then
and
From these formulae, as well as the well known fact that sorting is of complexity
, it is
easy to see that one can calculate the discrepancy in the one-dimensional case in
steps.
Using a memory versus speed tradeoff [34] it is possible to get the complexity down to
. In higher dimensions
calculating the discrepancy
is of complexity ,
making any reasonable empirical testing computationally infeasible. Probabilistic
algorithms [89] can be employed to calculate tight upper bounds for a given
.
What do we know about the behaviour of
with
increasing
? If the sequence of point is indeed uniformly distributed in
, then we
know that .
For a sequence of uniformly distributed random points we know that
with probability one. But in order to use the discrepancy as a
figure of merit for finite sequences, we need to know exactly how
converges for random sequences. Luckily, the following result (due to Kiefer [49])
provides us with the benchmark according to which we can judge the discrepancy
bounds derived for PRN.
Proposition 3.3 (Law of the iterated logarithm) Let
be a sequences of uniformly distributed random points in ,
then we have
where
is the Lebesgue measure on the space of all infinite sequences in .
The discrepancy is per definition an upper bound for the quasi-Monte Carlo
integration error for a very limited class of functions, namely the characteristic
functions of axis-parallel cubes. A classic result by Hlawka uses the discrepancy to
derive an error-bound for a large class of functions.
Proposition 3.4 (Koksma-Hlawka inequality [70]) If
has bounded variation
on
in the sense of Hardy and Krause, then for any
we have
Why is this inequality so important ? For the Monte Carlo numerical
integration, which is based on “random numbers”, one cannot derive an
a-priori
error bound on the integration error. It is only possible to state a probabilistic error
bound, a shortcoming that is often not acceptable. The inequality of Koksma-Hlawka
on the other hand, is a hard bound on the integration error. Thus in order to get such
a bound for the Monte Carlo method, one has to calculate the discrepancy for the
numbers used, which is not feasible in practice. The way out is to use a set of
numbers for which bounds on the discrepancy are known in advance, such as
-nets
or PRNGs for which such bounds are available.
On the other hand, if we want our PRNG to model a
distributed
random variable as closely as possible, the law of the iterated logarithm provides us with
the correct order of magnitude for the discrepancy. One can argue that any results
concerning the discrepancy of a particular generator which shows a rate of growth close to
is a
sign for the right amount of “randomness” in the generator. Empirical evidence seems
to support this argument. In any case, the discrepancy is certainly the most widely
used figure of merit in theoretical analysis of pseudorandom number generation
algorithms.
3.3.2 Auxiliary Results
In order to prove discrepancy bounds, we need a variety of auxiliary results.
Unfortunately it is not possible to include the proofs for these lemmata without
exceeding the scope of this thesis, as well as alienating the target audience. Thus we
will only list the results and give references to the proofs.
The basic approach to derive discrepancy bounds for PRNG is due to
Niederreiter [70], who established a link between the discrepancy of a finite
sequence of points with rational coordinates and certain exponential sums. As
most common PRNG use integer arithmetic combined with a final scaling
operation, this approach is perfectly suited for the study of the output of such
generators.
Niederreiter’s proof [70, §3.2] is elementary, although rather tricky. Hellekalek [39]
gave a proof based on dyadic harmonic analysis. A detailed proof can be found in
Weingartner [87].
In correspondence with the literature [71, 70], we will use the following definitions: For a
prime let
be the set of
all nonzero
with for
. For such
, put
with
for
nonzero and
. Furthermore,
set for
, and let
denote the standard
inner product of .
Although some of the Lemmata below do not need this restriction, we will consider
only the case of prime moduli here.
Lemma 3.1 For a prime
and ,
let
be the finite sequence .
Then
The following Lemma is due to Niederreiter [71, Lemma 2] which improves [70,
Corollary 3.11].
Lemma 3.2 Let
be a prime and let .
Suppose the real number
is such that
Then the discrepancy
of the finite sequence
satisfies
In order to derive the bound
for the EICG we need the following two Lemmata, the first one is due to Cochrane [7],
the second is a variant of the Bomberi-Weil bound for exponential sums (see Moreno
and Moreno [68, Theorem 2]):
Lemma 3.3 For any prime
and any integer
we have
Lemma 3.4 Let
be a rational function over
which is not of the form
with .
Let
be the number of distinct roots of the polynomial
in .
Then we have
where
and
if ,
and
and
otherwise.
The Koksma-Hlawka inequality can be used to derive a lower bound on the
discrepancy of a finite sequence of points. All that is needed is a function with a known
integral and bounded variation. In light of the previous lemmata it seems natural to
use a function for which the Monte Carlo integration can be expressed in terms
of exponential sums. The following result is due to Niederreiter [70, Cor.
3.17].
Lemma 3.5 For a prime
and ,
let
be the finite sequence .
Then, for any nonzero ,
we have
where
is the number of nonzero coordinates of .
Unfortunately, we cannot prove a lower bound on the generic sum
for finite sequences of points generated by an EICG. But we are
able to prove such bounds for a slightly different exponential sum
,
which we can link to sequences generated by an EICG, and which is a special case of
the sum in Lemma 3.5. This approach is due to Eichenauer-Herrmann and Niederreiter
[23]. All lemmata and theorems concerning lower bounds are taken from this
paper.
For
and
we define
|
| (3.11) |
and put .
Lemma 3.6 If
and
distinct, then
and
See [23] (Theorem 1 and Corollary 1) for the proofs, which are similar to the proofs of
Theorems 3.2 and 3.3. Besides these upper bounds, we know the average value of the
,
according to the next Lemma.
Lemma 3.7 Let
and ,
with fixed .
Then we have
Proof: We set .
With
we get
because we have
for
and
otherwise. __
Applying Lemma 3.5 on a finite sequence of points generated
by parallel streams of EICG according to Definition 3.1, and
we get
for
with and
. Similarly,
for
and
we have
|
| (3.13) |
3.3.3 Bounds
We now have the tools necessary to derive upper and lower bounds on the discrepancy
of finite sequences of points generated by parallel streams of EICG numbers. But as a
reference, let us first look at the result available for the LCG, which will once again
serve as a reference.
According to [70, Theorem 7.4] we have for the multiplicative
linear congruential generator the following statement: For
and for an average multiplier
, the discrepancy of the finite
sequence of -dimensional
points consisting of all
overlapping tuples from
obeys
where the implied constant depends only on
.
Upper Bounds
We first turn our attention to upper bounds; we will prove both bounds for
the full, as well as or parts of the period. These bounds are relevant in two
ways:
- A small discrepancy in the -dimensional
case guarantees the uncorrelatedness of these -tuples.
Basically, the EICG passes a generalized serial test, as the parallel streams
encompass more than just tuples formed from consecutive numbers.
- For -dimensional
quasi-Monte Carlo integration, a bound on the discrepancy equates to a
bound on the integration error.
Please note that the following theorems do not depend on the choice of any
parameters; they are valid for every single full period EICG. This is in sharp contrast
to the bounds known for the LCG, which is only deals with the average over all
multipliers, and thus tells us nothing about a particular generator. Furthermore, in the
case of the LCG no bounds are known for parts of the period in dimensions
.
As one can guess from the lemmata listed above, the proofs involve exponential
sums which need to be rearranged in a way to be able to use Lemma 3.4.
The following two theorems are due to Niederreiter [71].
Theorem 3.2 For ,
prime, and
set
based on the
of Definition 3.1. Then we have for the discrepancy of the finite sequence
the following upper bound:
Proof: For
put
We now restrict the sum to those terms where
by using the
same set
as in the proof of Theorem 3.1 as the summation domain. By noting that
and
using the triangle inequation we get
where is the rational
function over
given by
|
| (3.14) |
As all are nonzero, we
have . Furthermore,
as at least one of the
is nonzero, the uniqueness of the partial fraction decomposition for rational functions implies
that
and .
In order to apply Lemma 3.4, we have to show that
is not of
the form
with , where
denotes the algebraic
closure of the field ,
and denotes the field of
rational functions over .
If this were the case, we would have
with polynomials
over
and ,
and thus
|
| (3.15) |
Since we have demanded ,
cannot
divide or
, thus
must
divide . As
, that can only
be the case if
is a nonzero constant polynomial which implies
. Comparing the
degrees in (3.15) yields ,
which contradicts the degrees derived from (3.14). Thus we can apply Lemma 3.4, and
this leads to
|
| (3.16) |
The rest follows from Lemma 3.2. __
Theorem 3.3 For ,
prime, and let the
finite sequence
be like in Theorem 3.2. Then we have for the discrepancy of the first
points
the following upper bound:
Proof: Just as in the proof of Theorem 3.2 we need to derive a bound for an
exponential sum to be able to apply Lemma 3.2. This time the summation domain is
not ,
thus we need to rewrite the sum in a rather tricky way.
For
put
with for
. We can now
rewrite using
the fact that
evaluates to
for and
to
otherwise.
In the last line the summand for
was pulled out; the term
is the same as in the proof of Theorem 3.2. As we need an upper bound on
, we
apply the triangle inequation, yielding
|
| (3.17) |
and examine each of the terms on the right side.
We want to apply Lemma 3.4 on the rightmost term: For
we
have, by the same argument as following (3.14)
where is the rational
function over
given by
Once again, we claim that
is not of the form with
a rational function .
From the definition of
and we
have and
, as all the
neither the
nor
can be zero. For if we had
with polynomials
over and
, then the argument
following (3.15) shows that
is a nonzero constant polynomial. Thus we have
for suitable
with .
Comparing the degrees of the polynomials in this equation we get
, which
implies ,
hence .
This contradiction proves that we can apply Lemma 3.4, yielding
|
| (3.18) |
Furthermore, by rewriting the sum over
using some elementary
equivalences like ,
we get
We now return to (3.17) to put the pieces together. Combining everything with an
application of Lemma 3.3 we get
for all ,
and thus we can apply Lemma 3.2 to obtain the desired upper bound on
.
_
Lower Bounds
The theorems covering lower bounds are formulated in a different way. Instead of
giving hard bounds for all EICG, these theorems state how many EICGs there must
be exceeding a threshold value for the discrepancy. This kind of statement follows from
the basic approach to the problem, namely combining upper bounds on exponential
sums with their average values.
Lower bounds guarantee that the PRN are not perfectly equidistributed, they
contain the irregularities found in “random” numbers, too.
The following three theorems are due to Eichenauer-Herrmann and Niederreiter
[23].
Theorem 3.4 Let ,,
and
be fixed. Let ,
and set
Then there exist more than
values of
such that for -tuples
from the corresponding parallel stream of EICG numbers with
and
we have
Proof: We rewrite the theorem in terms of
by using (3.12).
Thus we have ,
and with
, and we need to show
that there are more than
values for
such that .
Now suppose there exist at most
values of with
, i.e., there
exist at least
values of with
. From Lemma
3.6 (with ) we
know that for
every . Hence,
observing that
contributes nothing to the sum, we obtain
which contradicts Lemma 3.7 (with ,
, and
).
_
Theorem 3.5 Let ,,
and an integer
with
be fixed and set
for . Then there
exist more than
values of such
that for -tuples
from the corresponding parallel stream of EICG numbers with
and
we
have
Proof: The proof is analogous to the last one. The only real difference is the handling of
, where we need to
apply Lemma 3.6 with .
_
Using (3.13) instead of (3.12) we get a slightly different result. As the proof
contains no new ideas, we omit it, too.
Theorem 3.6 Let
and
be fixed. For real numbers
fulfilling
set
Then there exist more than
values of
such that for -tuples
from the corresponding parallel stream of EICG numbers with
and
we have
Restricting oneself to the ordinary serial test, i.e. is considering only overlapping
-tuples
instead of vectors from parallel streams, it is possible to improve Theorem 3.6. See [23,
Corr. 9] for details.
3.4 Other Results
For congruential generators modulo a prime
, the
following definition, due to Niederreiter [70], specifies another criteria which can be
used to classify PRNGs.
Definition 3.4 For given ,
a congruential generator producing the sequence
passes the -dimensional
lattice test if the vectors ,
span the -dimensional
vector space ,
where
Theorem 3.7 An EICG with modulus
passes the -dimensional
lattice test exactly for all .
This is the optimal behaviour under this test.
Proof: As explained in 1.3.4, one can visualize any congruential generator modulo
with period length
as a permutation
polynomial mapping
to .
In the case of the EICG, this polynomial has degree
as we
can write the the EICG formula as
according to the theorem of Euler-Fermat. The rest follows immediately from a
theorem by Eichenauer, Grothe, and Lehn [13], which can also be found in Niederreiter
[70, Theorem 8.2]. __
Chapter 4
Empirical Tests
As explained is section 2.3.2, testing a pseudorandom number generator is
a tricky task. Even if one decides which properties one wants to test for,
designing the test itself involves a fair amount of statistic knowledge as to
how the test should be parameterized as well as how the results should be
judged.
In this chapter, we will try to give a survey of empirical tests concerning the
EICG carried out by various authors. Since it will be inappropriate to spend too much
time on discussing all design decisions in detail, we will only describe the motivation,
the test procedure, and the results. For more information we refer to the original
authors.
Another compilation of empirical test results concerning inversive generators can be
found in [21].
4.1 Digit Test
The Digit Test, due to Leeb
[58, 26, 61], tries to assess the distribution quality of a PRNG by looking at the
-adic representation of its
output. If we only allow ,
one digit in base
corresponds to
binary digits, which we can obtain by cutting out
consecutive
bits in the computer representation of the numbers. This is a very efficient procedure which
can be done by simple bitwise AND and shift operations. Let’s visualize this by an example,
using as
the base and selecting the second digit which is corresponds to the three bits starting at
position .
|
|
|
|
| Decimal | Binary | Base 8 | selected digit |
|
|
|
|
| 0.5859375 | 0.100 101 10 | 0.454 | 5 |
| 0.82421875 | 0.110 100 11 | 0.646 | 4 |
| 0.21484375 | 0.001 101 11 | 0.156 | 5 |
| 0.765625 | 0.110 001 00 | 0.610 | 1 |
| 0.16015625 | 0.001 010 01 | 0.122 | 2 |
| 0.48046875 | 0.011 110 11 | 0.366 | 6 |
|
|
|
|
| |
Ideally, we expect the last column to be uniformly distributed over all possible
digits. Furthermore, we can assume that if the original numbers are uncorrelated, this
will hold for the sequence of digits, too. On the other hand, if we can prove that
something is wrong with the digit sequence, this does not shed a good light on the
original numbers.
What have we gained by mapping numbers to digits ? Basically this mapping plays
the role of the “bins” discussed on page and . As discussed there, this mapping is
used to make the problem manageable by drastically reducing the number of possible
values for each number. Now we can easily count the occurrences of each different digit
and perform correlation tests on them.
As a correlation test Leeb used the idea of the serial test (see p. ) with non-overlapping
-tuples. To measure the
distribution of the -tuples,
a test was used;
the resulting -value
was called ,
the level-1 test statistic. This procedure was repeated 64 times, and all the
values
were compared to their expected distribution by a two-sided Kolmogorov-Smirnov test,
yielding ,
the level-2 test statistic on which we will focus in the graphics.
Let’s summarize all the parameters which must be specified to turn the abstract
idea of the Digit Test into a computer program.
- First of all, we have to specify the generator we want to test. Leeb used both
a selection of popular linear congruential generators as well as inversive
generators. In Table 4.2 the LCG are sorted according to their performance
in the spectral test [9]; the smaller the value for
the better is the lattice structure of the generator in dimension 3.
- Next, the number of bits to cut out is selected. This block-length
determines the base ()
of the digits to test. In his calculations, Leeb used .
- Now that we know how many bits we want from each number, the next
step is to determine which bits to cut out. Leeb termed this parameter the
block-start ,
which he chose from the set .
- We are now able to generate a sequence of digits (or bit-blocks) according
to the parameters specified so far. The next step is to combine consecutive
digits to vectors by forming non-overlapping -tuples.
Leeb chose to use dimensions
up to 10. As the dimension increases, the number of bins needed for the
counting process grows exponentially; thus Leeb had to restrict the range of
the block-length
with increasing
in order to keep the computation feasible.
- Next we need to determine how many -tuples
we should generate. The common rule of thumb for
tests is to make sure that the each of the
bins can expect at least 5 hits. As we expect equidistribution amongst the
bins, we get a lower bound on how many tuples we should generate. Leeb
decided to generate
tuples, which were in turn generated using
numbers from the PRNG.
- We have now finished the first level ()
of the Digit Test. For the second level (),
we need to repeat the above procedure with a distinct sample of PRN to be
able to use the KS test. Leeb chose to use 64 repetitions which guarantees
that the KS approximation is valid.
It should be clear by now that the hierarchical design of the complete testing
procedure results in huge resource requirements both computationally as well as
memory-wise to actually run the test. See Table 4.1 for the actual parameters used,
and Table 4.2 for the generators tested. The computations were carried out using the
pLab [57] PRNG testing framework, which is based on the author’s generator
library.
|
|
| | digit test parameters
|
|
|
| | dimension | block-start | block-length |
|
|
|
|
|
| | 1 | | |
| 2 | | |
| 3 | | |
| 4 | | |
| 5 | | |
| 6 | | |
| (7) | | |
| (8) | | |
| | | |
|
|
| | |
| Table 4.1: | Digit test parameters (parentheses indicate that only
was computed) |
|
|
|
|
| | generators
|
|
|
|
| | nickname | generator | period | |
|
|
|
|
|
|
|
| | RANDU | | | |
| ANSI | | | |
| MINSTD | | | |
| FISH | | | |
| EICG1 | | | |
| ICG | | | |
|
|
|
| | |
| Table 4.2: | Generators used in the Digit test |
|
For the graphics, the
value was transformed according to the expected
distribution to yield a value which should be asymptotically equidistributed.
Thus all points in the graphics on the left hand side should vary
freely between 0 and 1. Values close to 0 signify a distribution of the
-tuples
which is much to well-balanced, whereas values close to 1 indicate
gross irregularities. The right hand graphics depict the KS-statistic
, for which the critical
region at the level
of significance is .
Any generator which features high values there (especially when reaching the cut-off
point 2 in the graphics) fails in the test.
As Leeb in [58], we present here only a selection of the results, namely those for dimension
. For each generator,
the values of
and
were varied.
Interpretation:
The digit test seems to be sensible to intrinsic properties of the LCG, as even
the best one (FISH) fails the test for certain parameters. Leeb conjectures in
[58] that the digit test is sensible on grid structures or long-range correlation
as these are two features which are present in all LCG but are proven to
be absent in inversive generators. Especially the lattice quality parameter
seems
to correlate with the digit test results. The better the lattice is (small values for
), the higher
the values for
and
must be to uncover deficiencies in the generator.
4.2 Overlapping Serial Test
The overlapping serial test, first proposed by Marsaglia [66] as the “M-tuple test”, is in
its basic setup quite similar to the digit test described above. The main difference is to
use overlapping tuples. This modification is rather small in the implementation, but
requires some statistical work to calculate the expected distribution as the tuples are
no longer independent.
We will describe here the empirical tests done by Wegenkittl [85, 86, 61]. As the
testing procedure was very similar to the digit test setup, we will only list
the differences here. Whereas Leeb in the digit test used only one way to
extract bits from the stream of pseudorandom numbers, Wegenkittl used two:
- Digit(Start, Length) is the same method as used in the digit test, namely
cutting out Length bits starting at position Start from each number.
- BitStream(Number, Length) extracts more than one set of Length bits from
each number, thus reducing the number of PRN needed to generate the
tuples. This is achieved by cutting out Number times Length bits starting
from the first bit. Furthermore, this method makes it feasible to test the
numbers for correlations between the high-order and low-order bits.
This time these blocks of bits were used to generate variable
number of tuples. Whereas in the digit test the sample size
was always tuned to the
subsequent test, Wegenkittl
generated up to tuples. From
these tuples, a modified
statistic
was computed, resulting in the test-statistic
. Whereas the “normal
test statistic” does
not converge to a
distribution for overlapping tuples due to the correlations, this modified one does (see [85, p.
57] for details). This procedure was repeated 32 times and the resulting empirical distribution
of the
values was compared to the theoretical one using a KS test.
The following graphics
depict the results for all the generators used in the digit test, as well as for EICG7 which
stands for .
The left hand diagrams show the values for each of the
calculated
test
statistics as the lightness of each small rectangle. A white square signifies a low value for
, meaning
perfect equidistribution of the tuples, whereas a black one signifies extreme deviations. The
transformation
lightness was chosen in such way that each gray-scale level should be equally likely.
Unfortunately, these diagrams are not available for all parameters.
In the right hand diagrams these
values were distilled into one single KS value representing
the quality of their distribution. The critical region at the
level of significance
is in this case .
Interpretation:
Like the Digit Test, the overlapping serial test does uncover deficiencies in the
linear generators. Whereas the setup in the Digit Test focused on the number of bits
you can take from a number while still getting good distributions, Wegenkittl turned
his attention to the number of tuples one can generate before the PRNG fails. The
results are basically the same: even the best LCG has a limited load-capability; if you
start to do heady-duty computations using many PRN you must be careful not
to run into the breaking point of the LCG. The traditionally rule of thumb
concerning which percentage of the period length one can safely use (up to
)
seems to be sound for the LCG.
The inversive generators are not perfect either, even they tend to fail
the test at some point. But their load-capability is much better. Even when
taking a high number of samples, their distribution quality decreases quite
slowly.
4.3 Run Test
A completely different kind of empirical test is the run test. The basic idea behind this
test is to check if the occurrences of runs conforms to its expected value. There is a
variety of different ways to implement this idea, but we will only describe the idea and
Entacher’s implementation [24].
First of all, what do we mean by “runs” ? In a binary context, that is sequence
consisting only of two symbols, a run is defined as a subsequence consisting only of one
symbol. For example, consider the sequence
in which the brace indicate the runs.
As the common pseudorandom sequences are far from being binary, one has to
transform them first. A straight forward way of doing this is
which is binary as
for PRNG we consider. A run of 1s of length
corresponds to a monotonically increasing subsequence of length
in the
original sequence called a “run up”. The distribution properties of these runs in a
sequence of “really random numbers” is well known.
According to Wolfowitz [63] (see also Knuth [50, p. 68]) Entacher constructed an asymptotically
-distributed
test statistic
which involves counts for ascending runs up to length
.
The calculation done by Entacher involved evaluating
100
times for each generator and testing this empirical distribution against the expected
one using a KS test.
We will focus on Entacher’s results concerning the behaviour of LCGs and EICGs.
The list of generators tested include the previously defined generators FISH, ANSI,
MINSTD, and RANDU, as well as two other LCGs with a bad lattice structure:
LCG5 and
LCG6. As examples for the
EICG Entacher used
with parameter
which he labeled EICG1 to EICG6.
The following figures
depict the results; The sample size was varied between
and
(the labels
are ),
the height of each square shows the resulting KS statistic. If the square is coloured
dark gray, then the KS statistic exceeds the critical value for the significance level
0.01.
Interpretation:
The run test seems to be able to distinguish good LCGs from bad ones. All
basically randomly chosen EICG pass the test without any problems, showing again
that the EICG is not sensitive to the parameter selection.
Another conclusion from this test is that subsequences taken by a leap frog
technique are save when using EICGs, whereas such sequences taken from an
LCG may exhibit a bad lattice and can fail the run test. See an upcoming paper from
Entacher [24] for details.
4.4 Weighted Spectral Test
As mentioned on page , the weighted spectral test is a promising new approach to
assess the quality of pseudorandom numbers, see Hellekalek [40, 41], Hellekalek and
Niederreiter [46], and Hellekalek and Leeb [44]. One numerical realization of
the weighted spectral test is the diaphony, see Hellekalek and Niederreiter
[46].
Both the diaphony [90] as well as the classic spectral test [9] approach the point set
from a Fourier point of view, looking for any disturbances in the spectrum. If the point
set has lattice structure (as in the case of LCGs), the first wavelength which yields a
non-zero Fourier coefficient corresponds to the largest distance between hyperplanes.
Where the classic spectral test targets just this wavelength, the diaphony tries to
include more information, namely a weighted sum over all possible wavelengths. High
wavelengths (which correspond to low frequencies) in the point set indicate
a large scale imbalance, whereas high frequencies target fine structures in
the set. As these fine structures are unavoidable at the certain point, higher
frequencies are considered less important and thus will contribute little to the
diaphony.
So basically the -dimensional
diaphony is a weighted sum over the correlation coefficients of the point set, which are basically
the Weyl sums
we encountered in Section 3.3, see [41] for details.
There are close ties between the discrepancy and the diaphony. One can bound one
in terms of the other (see Stegbuchner [79]), one can interpret it, too, as integration
error (see James, Hoogland and Kleiss [47]), and it is possible to derive Lemmata
similar to those in section 3.3.2 (see [41]).
Whereas it is virtually impossible to do any reasonable empirical
studies with discrepancy due to its computational complexity of
, the diaphony
only needs
steps to calculate it. Thus it is possible to conduct empirical test using this figure of
merit. In the following we will describe the results obtained by Hellekalek [40].
The test procedure was as follows: For a given generator, for a given dimension
, and a given
sample size ,
the diaphony
was evaluated for 20 samples of non-overlapping
-tuples. As the expected
value for equals
, Hellekalek multiplied
the diaphony by
to get the same expected value for all sample sizes, see Leeb [60] for the theoretical
distribution.
In the graphics, the abscissa
shows the sample size as
and the ordinate the average value over the 20 samples. For each generator from the
now familiar set (see Table 4.2) the calculation was done in dimensions 2
(), 3
(), 4
(), 5
(), and
dimension 6 ().
4.5 Other Results
Frank Härtel [37] implemented an impressive array of PRNG and compared their
performance under a variety of statistical tests. Unfortunately he used only one
EICG (), whose
modulus ()
is far too small to be able to compete with generators featuring a period length of
. We
will therefore not elaborate on his results.
Both Eichenauer-Herrmann and L’Ecuyer presented results of empirical test
concerning the minimal distance between vectors of PRN on the MC&QCM’96
conference in Salzburg. Although the results have not been published yet, one can
summarize them as follows: due to their lattice structure, LCGs are not able to
simulate the correct behaviour of the test statistic whereas EICGs with the same
period length pass this test with flying colors. I refer to the upcoming proceedings for
details.
Chapter 5
Implementation
This section discusses the implementation of the EICG pseudorandom number
generator using a standard procedural programming language. We will use C syntax for
the code printed here.
The algorithms presented here were used to write a generic and portable
PRNG library which implements not only the EICG, but other congruential
generators, too. This library (written in ANSI C) is available on the Internet from the
pLab WWW server at http://random.mat.sbg.ac.at/.
5.1 Overview
If we look at the definition of the EICG (see p. 1.3.4), we see that generating
the numbers is a two step procedure. First we have to compute the
, a calculation operating
in the finite field
which can be done by standard integer calculation modulo
. The second step is
the scaling operation ,
which we will implement as a straight forward floating point division.
We will thus focus on the first step, which includes the following three
operations
- Inversion modulo
- Multiplication modulo
- Addition modulo .
How they are best implemented depends on how numbers are represented in the
computer. We use integer arithmetic based on the native integer format of the
computer. Most current workstations use 32-bit integers which can hold numbers from
to
.
This limits the choice of the modulus to values smaller than
, a common choice is
the Mersenne prime .
Large values for
give the resulting PRN a fine resolution, but one has to pay for this with an increase in
calculation time. If this resolution, as well as the period length it implies, are not
adequate, one can use the technique of combining generators (see p. ), to generate
even better pseudorandom numbers.
5.2 Modular Inversion
First we turn to the problem of modular inversion (denoted throughout this text by overlining
() the
operand) which is defined as
where is the uniquely
defined element of
such that .
The special case is easily
handled, what remains is to find
for .
There are two different ways to compute the inverse, one of them is to utilize the fact
that
by the well-known theorem of Euler–Fermat, and thus
holds. In our case here the modulus is prime, thus
, Euler’s totient
function, is equal to ,
which gives us
Evaluating
is a well-known exercise in computational number theory (e.g. in the RSA cryptosystem).
It can be solved in logarithmic time [8, p. 829], but intermediate results exceed the
domain .
This fact renders an implementation difficult because of the limited integers available
on a computer.
A different approach is to use an extended version of Euclid’s algorithm.
This algorithm is usually used to calculate the greatest common divisor
of two numbers, but it can also be used to calculate the integers
and
which fulfill the linear
diophantic equation .
By substituting
for and
observing that ,
one gets
which can be rewritten as
This algorithm to calculate
and
is based on the following recursion: The division with remainder
is used to
calculate
and . If we
can find
and which
fulfill ,
then and
will satisfy
. Since
and
the question
how to find the
and
will lead to a trivial case.
Figure 5.1 shows a straight-forward recursive implementation of the extended
Euclid’s algorithm. Figure 5.2 demonstrates how the modular inversion can be based
on rec_eeuclid.
This recursive implementation is not very efficient due to the overhead caused by
the repeated function calls. Although rec_eeuclid is not end-recursive, it is possible
to rewrite it as an iterative function [50]. Figure 5.3 is a C implementation of the
modular inversion using this method. A further optimization [77, p. 521] is to unroll
the loop twice to avoid unnecessary swapping of the variables in each iteration.
Gordon [35] describes a modification which uses shift operations to avoid
multiplications and divisions. This does pay on certain computers, for example on
SPARC, R4000, or Alpha AXP based systems this approach is faster. On the other
hand, the division on the i486 is comparatively fast, thus the original version runs
faster there.
The number of recursive calls in Euclid’s algorithm is of the order
,
see [8, p. 810]. An equivalent statement is, that the arguments of
these calls decrease exponentially. Another way to put this is that
rec_eeuclid will need about the same number of recursive calls to get from
to
as it needs
from
to the end of the recursion.
This observation leads to another technique to speed up the computation of the multiplicative
inverse: For all
smaller than some threshold we use a table of precomputed values for
and
instead of continuing the recursion. This way some recursive calls can be
avoided.
|
|
|
|
| | Threshold | Memory used | Avg. Steps | Std.dev. | Time |
|
|
|
|
| | No Table | - | 17.57 | 3.27 | 43.76 s |
|
|
|
|
| | 16 | 256 Bytes | 16.72 | 3.10 | 45.40 s |
| 32 | 1 KByte | 16.11 | 3.04 | 43.84 s |
| 64 | 4 KByte | 15.52 | 2.98 | 42.32 s |
| 128 | 16 KByte | 14.93 | 2.92 | 41.03 s |
| 256 | 64 KByte | 14.35 | 2.86 | 39.71 s |
| 512 | 512 KByte | 13.77 | 2.80 | 39.31 s |
|
|
|
|
| | |
| Table 5.1: | Average number of recursive calls in Euclid’s Algorithm. |
|
To test the advantages of this approach, we compared it with the optimized
iterative implementation. Table 5.1 lists the timings of my test case, that is calculating
the multiplicative inverses of 2147483 uniformly distributed numbers modulo
.
As long as the threshold is not larger than 256, a byte is enough to hold
an element of the table. A threshold of 512 forces the program to resort to
16-bit integers which doubles the memory requirements. It is hard to make a
general statement which threshold is best, too much depends on the cache size,
memory access speed, and on memory available. We have set the default to
256, which seems to result in a reasonable tradeoff between memory and
speed.
Our experience has shown that there is no single “best” algorithm, too much
depends on the relative execution speed of various elementary operations. Thus our
implementation includes three different algorithms as well as a profiling program
which can be used to select the one which is running fastest on the user’s
computer.
5.3 Modular Multiplication
The problem of evaluating
lies in the limited range of the integers available in common programming languages. The
intermediate result
of the straightforward implementation is very likely not to fit in
machine size integers, so one has to devise an algorithm to calculate
in which all intermediate results are representable on a
-bit
computer.
One approach is the following algorithm due to Bratley, Fox, and Schrage [4, Sec. 6.5.2] which
can compute
if .
The idea is to factor the modulus, but since this is not possible with primes, one has to
deal with remainders, too. Let
where
Then one can rewrite
as
If , which is a direct
consequence of ,
evaluating
does not pose a numerical problem, for
and
and thus . Since
evaluating
is unnecessary,
because
iff
and
iff .
This leads to the following algorithm:
and
can be precomputed,
calculating
and
requires on some computers only one instruction, so this is a very efficient
algorithm.
For the usual choice of
for the above can
be applied for all .
If is
smaller than that, then the limitation that all intermediate results should be between
and
is unnecessarily tight.
On a -bit computer
all integers between
and
(exclusive) are representable. If we loosen the restriction on
from
to
, the term
is no longer
bounded by . But it
can be shown that
is an upper bound:
We can now conclude that
and .
Thus one possible algorithm is this:
- Calculate
and
-
- while()
The while loop can execute at most
times. L’Ecuyer and Côté [56] observed that in the average case very few iterations
are executed, thus this algorithm is efficient.
If
is not restricted in any way (except of course by the requirement
)
one can use decomposition to reduce the multiplication to cases for
which we already have solutions. This can be achieved by writing
in
base ,
where
(usually 15 on current 32-bit computers):
with ,
and .
Then
In all four products modulo one
of the factors is bounded by ,
so the previously discussed algorithm can be applied. Figure 5.4 shows a C
implementation of this method. It is used whenever it is not possible to resort to a
simpler algorithm.
5.4 Modular Addition
Modular addition is simple to solve, though it is not trivial. A straightforward
implementation might look like this:
-
- if ()
then
This is correct, as long as
is still fully representable with the data type used. Assuming that
the usual signed integer type is used, an overflow would occur if
is negative. It cannot
happen that is positive in
spite of an overflow, since
and are both smaller
than (assuming
a -bit computer)
and wraps to
. If we detect an overflow,
subtracting will bring the
result back into the interval .
Thus this
-
- if (
or )
then
is a correct implementation.
Chapter 6
Summary
Let us quickly summarize the main points of this thesis.
- The application defines the quality criteria for the PRNG. There
is no such thing as the perfect (“one size fits all”) pseudorandom number
generator; one should always consider the application when choosing a
generator.
- Testing a PRNG is a tricky task. While testing can increase the
confidence in the generator, it is often not possible to construct a test
which targets the same properties in the number as will be relevant in the
application.
- Do not rely on a single family of PRNG ! As a consequence of the
previous two remarks, one should never trust the result of a simulation
without verification runs using a completely different PRNG.
- The definition of the EICG.
Let
be a (large) prime and .
The explicit inversive congruential generator (abbreviated as “EICG”) with
parameters
and
defines a sequence
in
by
and a sequence
of pseudorandom numbers in
by
where
denotes the multiplicative inverse modulo
extended by .
- The choice of parameters is easy for the EICG. As long as ,
the period length will always be .
There are no theoretical results indicating that some parameters might
result in bad distribution properties. This is a major advantage over the
LCG, where every set of parameters must be extensively screened using the
spectral test.
- EICGs with the same modulus are closely related. These relation
include shifting the sequence (different
or ),
and taking every -th
number (different value for ).
- Taking subsequences from EICGs is safe. As a consequence of the last
two statements, the EICG is perfectly suited to generate streams of PRN.
This can be done by taking either every -th
number or starting at a different position in the stream. In both cases, the
individual streams are guaranteed to be uncorrelated.
- Tuples of EICG numbers show strong non-linear properties. See
Theorems 3.1 and 3.7 for details.
- The order of magnitude of the discrepancy of
-tuples
of EICG numbers is close to the optimal value. For true random
number we have an order of magnitude between
and .
Examining tuples formed using the full period of the EICG we get
as an upper bound, and an existence statement which implies that this
bound is the best possible up to the logarithmic factor.
For parts of the period we get similar results: as an upper bound we have
,
and we can show the existence of EICGs with
for some constant .
- EICGs perform well in empirical tests. In all comparisons to linear
generators with about the same period length the inversive generators have
clearly proved their superiority.
- The EICG is not particularly difficult to implement. Short and
efficient algorithms for all steps involved have been published. A portable
implementation (ANSI-C) is available from the author.
- The EICG algorithm runs at a reasonable speed. The multiplicative
inversions takes about
steps; the EICG is thus considerably slower than the LCG. Whether this
difference is noticeable in the overall computation time depends heavily on
the amount of processing done in the simulation problem itself.
- Combining EICGs is safe. Using compound techniques it easy to
achieve long periods; excellent properties of the resulting numbers are
guaranteed [18, 19].
Bibliography
[1] S.L. Anderson. Random number generators on vector supercomputers
and other advanced architectures. SIAM Rev., 32:221–251, 1990.
[2] D.A. André, G.L. Mullen, and H. Niederreiter. Figures of merit for
digital multistep pseudorandom numbers. Math. Comp., 54:737–748, 1990.
[3] K. Binder and D.W. Heermann. Monte Carlo Simulation in Statistical
Physics. An Introduction. 2nd corr. ed. Springer-Verlag Heidelberg New
York, 1992.
[4] P. Bratley, B. L. Fox, and L. E. Schrage. A Guide to Simulation.
Springer Verlag, second edition, 1987.
[5] G.J. Chaitin. Randomness and mathematical proof. Sci. Amer.,
232:47–52, 1975.
[6] Wun-Seng Chou. On inversive maximal period polynomials over finite
fields. Appl. Algebra Engrg. Comm. Comput., 6:245–250, 1995.
[7] T. Cochrane. On a trigonometric inequality of Vinogradov. J. Number
Th., 27:9–16, 1987.
[8] Thomas H. Corman, Charles E. Leiserson, and Ronald L. Rivest.
Introduction to Algorithms. The MIT Press, first edition, 1989.
[9] R.R. Coveyou and R.D. MacPherson. Fourier analysis of uniform random
number generators. J. Assoc. Comput. Mach., 14:100–119, 1967.
[10] A. De Matteis and S. Pagnutti. Parallelization of random number
generators and long-range correlations. Numer. Math., 53:595–608, 1988.
[11] G. Dueck and T. Scheuer. Threshold Accepting: A General Purpose
Algorithm Appearing Superior to Simulated Annealing. Journal of
Computational Physics, pages 161–175, 1990.
[12] W.F. Eddy. Random number generators for parallel processors. J. Comp.
Appl. Math., 31:63–71, 1990.
[13] J. Eichenauer, H. Grothe, and J. Lehn. Marsaglia’s lattice test and
non-linear congruential pseudo random number generators. Metrika,
35:241–250, 1988.
[14] J. Eichenauer and J. Lehn. A non-linear congruential pseudo random
number generator. Statist. Papers, 27:315–326, 1986.
[15] J. Eichenauer-Herrmann. Statistical independence of a new class of
inversive congruential pseudorandom numbers. Math. Comp., 60:375–384,
1993.
[16] J. Eichenauer-Herrmann. Nonoverlapping pairs of explicit inversive
congruential pseudorandom numbers. Monatsh. Math., 119:49–61, 1995.
[17] J. Eichenauer-Herrmann. Modified explicit inversive congruential
pseudorandom numbers with power of 2 modulus. Statistics and Computing,
6:31–36, 1996.
[18] J. Eichenauer-Herrmann and F. Emmerich. A review of compound
methods for pseudorandom number generation. In P. Hellekalek,
G. Larcher, and P. Zinterhof, editors, Proceedings of the 1st Salzburg
Minisymposium on Pseudorandom Number Generation and Quasi-Monte
Carlo Methods, Salzburg, Nov 18, 1994, volume ACPC/TR 95-4 of
Technical Report Series, pages 5–14. ACPC – Austrian Center for Parallel
Computation, University of Vienna, Austria, 1995.
[19] J. Eichenauer-Herrmann and F. Emmerich. Compound inversive
congruential numbers: an average-case analysis. Math. Comp., to appear,
65:215–225, 1996.
[20] J. Eichenauer-Herrmann and H. Grothe. A remark on long-range
correlations in multiplicative congruential pseudo random number
generators. Numer. Math., 56:609–611, 1989.
[21] J. Eichenauer-Herrmann and E. Herrmann. A survey of quadratic and
inversive congruential pseudorandom numbers. Submitted to Proceedings
of the Second International Conference on Monte Carlo and Quasi-Monte
Carlo Methods in Scientific Computing, Salzburg, July 9–12, 1996.
[22] J. Eichenauer-Herrmann and K. Ickstadt. Explicit
inversive congruential pseudorandom numbers with power of two modulus.
Math. Comp., 62:787–797, 1994.
[23] J. Eichenauer-Herrmann and H. Niederreiter. Bounds for exponential
sums and their applications to pseudorandom numbers. Acta Arith.,
67:269–281, 1994.
[24] K. Entacher. Selected random number generators in run tests. Preprint,
Institut für Mathematik, Universität Salzburg, Austria, 1996.
[25] K. Entacher and P. Hellekalek. Parallel stochastic simulation: inversive
pseudorandom number generators. In G. De Pietro and P. Zinterhof
A. Giordano, M. Vajteršic, editors, Proceedings of the International
Workshop Parallel Numerics 95, Sorrento, Italy, September 27–29, 1995,
pages 1–14. IRSIP Institute of the NRC of Italy, Naples, 1995.
[26] K. Entacher and H. Leeb. Inversive pseudorandom number generators:
empirical results. In Proceedings of the Conference Parallel Numerics 95,
Sorrento, Italy, September 27–29, 1995, 1995.
[27] G.S. Fishman. Multiplicative congruential
random number generators with modulus
:
an exhaustive analysis for
and a partial analysis for .
Math. Comp., 54:331–344, 1990.
[28] G.S. Fishman and L.R. Moore. A statistical evaluation of
multiplicative congruential random number generators with modulus
.
J. Amer. Statist. Assoc., 77:129–136, 1982.
[29] G.S. Fishman and L.R. Moore. An exhaustive analysis of
multiplicative congruential random number generators with modulus
.
SIAM J. Sci. Statist. Comput. (see also the Erratum, ibid. 7(1986), p.
1058), 7:24–45, 1986.
[30] M. Flahive and H. Niederreiter. On inversive congruential generators
for pseudorandom numbers. In G.L. Mullen and P.J.-S. Shiue, editors, Finite
Fields, Coding Theory, and Advances in Communications and Computing,
pages 75–80. Dekker, New York, 1992.
[31] Mark Fleischer. Simulated Annealing: Past, Present, and Future. In
Proceedings of the 1995 Winter Simulation Conference, pages 155–161, 1995.
[32] J. Foley, A. van Dam, S. Feiner, and J. Hughes. Computer Graphics:
Principles and Practice. Addison-Wesley, second edition, 1990.
[33] I. Goldberg and D. Wagner. Netscape SSL implementation cracked!
Available on the WWW at
http://tezcat.com/web/security/items/ssl-news.txt.
[34] T. Gonzales, S. Sahni, and W.R. Franta. An efficient algorithm for
the Kolmogorov-Smirnov and Lillefors tests. ACM Trans. Mathem. Softw.,
3:60–64, 1977.
[35] J. Gordon. Fast Multiplicative Inverse in Moduar Arithmetic. In H. J.
Beker and F. S. Piper, editors, Cryptography and Coding. Oxford Clarendon
Press, 1989.
[36] J.H. Halton. Pseudo-random trees: multiple independent sequence
generators for parallel and branching computations. J. Comp. Physics,
84:1–56, 1989.
[37] F. Härtel. Zufallszahlen für Simulationsmodelle. PhD thesis,
Hochschule St. Gallen für Wirtschafts-, Rechts- und Sozialwissenschaften,
St. Gallen, 1994.
[38] S. Heinrich. Efficient algorithms for computing the
discrepancy. Interner Bericht, Fachbereich Informatik, Universität
Kaiserslautern, 1995.
[39] P. Hellekalek. Study of algorithms for primitive polynomials. Report
D5H-1, CEI-PACT Project, WP5.1.2.1.2, Research Institute for Software
Technology, University of Salzburg, Austria, 1994.
[40] P. Hellekalek. Correlations between pseudorandom numbers: theory and
numerical practice. In P. Hellekalek, G. Larcher, and P. Zinterhof, editors,
Proceedings of the 1st Salzburg Minisymposium on Pseudorandom Number
Generation and Quasi-Monte Carlo Methods, Salzburg, Nov 18, 1994, volume
ACPC/TR 95-4 of Technical Report Series, pages 43–73. ACPC – Austrian
Center for Parallel Computation, University of Vienna, Austria, 1995.
[41] P. Hellekalek. On correlation analysis of pseudorandom numbers.
Submitted to Proceedings of the Second International Conference on Monte
Carlo and Quasi-Monte Carlo Methods in Scientific Computing, Salzburg,
July 9–12, 1996, 1996.
[42] P. Hellekalek and K. Entacher. Revised implementation and testing of
the algorithms for IMP-polynomials. Report D5H-3, CEI-PACT Project,
WP5.1.2.1.2, Research Institute for Software Technology, University of
Salzburg, Austria, 1995.
[43] P. Hellekalek and K. Entacher. Tables of IMP-polynomials. Report
D5H-4, CEI-PACT Project, WP5.1.2.1.2, Research Institute for Software
Technology, University of Salzburg, Austria, 1995.
[44] P. Hellekalek and H. Leeb. Dyadic diaphony. To appear in Acta
Arithmetica, 1996.
[45] P. Hellekalek, M. Mayer, and A. Weingartner. Implementation of
algorithms for IMP-polynomials. Report D5H-2, CEI-PACT Project,
WP5.1.2.1.2, Research Institute for Software Technology, University of
Salzburg, Austria, 1994.
[46] P. Hellekalek and H. Niederreiter. The weighted spectral test: diaphony.
In preparation, 1996.
[47] F. James, J. Hoogland, and R. Kleiss. Multidimensional sampling
for simulation and integration: measures, discrepancies, and quasi-random
numbers. Preprint submitted to Computer Physics Communications, 1996.
[48] M.H. Kalos and P.A. Whitlock. Monte Carlo Methods, Volume I: Basics.
Wiley, New York, 1986.
[49] J. Kiefer. On large deviations of the empiric d.f. of vector chance
variables and a law of the iterated logarithm. Pacific J. Math., 11:649–660,
1961.
[50] D. E. Knuth. The Art of Computer Programming, Vol. 2: Seminumerical
Algorithms. Addison-Wesley, Reading, MA, second edition, 1981.
[51] L. Kuipers and H. Niederreiter. Uniform Distribution of Sequences.
Wiley and Sons, New York London Sydney Toronto, 1974.
[52] J. C. Lagarias. Pseudorandom numbers. Statistical Science, 8:31–39,
1993.
[53] P. L’Ecuyer. Random numbers for simulation. Comm. ACM, 33:85–97,
1990.
[54] P. L’Ecuyer. Testing random number generators. In J.J. Swain et al.,
editor, Proc. 1992 Winter Simulation Conference (Arlington, Va., 1992),
pages 305–313. IEEE Press, Piscataway, N.J., 1992.
[55] P. L’Ecuyer. Uniform random number generation. Ann. Oper. Res.,
53:77–120, 1994.
[56] P. L’Ecuyer and S. Côté. Implementing a Random Number Package
with Splitting Facilities. ACM Transactions on Mathematical Software,
17(1):98–111, March 1991.
[57] H. Leeb. pLab – a system for testing random numbers. In M. Vajteršic
and P. Zinterhof, editors, Proceedings of the International Workshop on
Parallel Numerics ’94, Smolenice, Sept. 19–21, pages 89–99. Slovak Academy
of Sciences, Institute for Informatics, 1994. Available on the internet at
http://random.mat.sbg.ac.at.
[58] H. Leeb. On the digit test. In P. Hellekalek, G. Larcher, and
P. Zinterhof, editors, Proceedings of the 1st Salzburg Minisymposium
on Pseudorandom Number Generation and Quasi-Monte Carlo Methods,
Salzburg, Nov 18, 1994, volume ACPC/TR 95-4 of Technical Report
Series, pages 109–121. ACPC – Austrian Center for Parallel Computation,
University of Vienna, Austria, 1995.
[59] H. Leeb. Random Numbers for Computer Simulation. Master’s thesis,
Institut für Mathematik, Universität Salzburg, Austria, 1995.
[60] H. Leeb. A weak law for diaphony. Rist++ 13, Research Institute for
Software Technology, University of Salzburg, 1996.
[61] H. Leeb and S. Wegenkittl. Inversive and linear congruential
pseudorandom number generators in empirical tests. submitted to ACM
Trans. Modeling and Computer Simulation, 1996.
[62] V. F. Lev. On two versions of -discrepancy
and geometrical interpretation of diaphony. Acta Math. Hungar.,
69:281–300, 1995.
[63] H. Levene and J. Wolfowitz. The covariance matrix of runs up and
down. Annals Math. Stat., 15 :59–69, 1944.
[64] R. Lidl and H. Niederreiter. Finite Fields. Addison-Wesley, Reading,
Mass., 1983.
[65] G. Marsaglia. Random numbers fall mainly in the planes. Proc. Nat.
Acad. Sci., 61:25–28, 1968.
[66] G. Marsaglia. A current view of random number generators. In
L. Brillard, editor, Computer Science and Statistics: The Interface, pages
3–10, Amsterdam, 1985. Elsevier Science Publishers B.V. (North Holland).
[67] L. Ming and P. Vitány. An Introduction To Kolmogorov Complexity
And Its Applications. Texts and Monographs in Computer Science. Springer
Verlag, New York, 1993.
[68] C.J. Moreno and O. Moreno. Exponential sums and Goppa codes: I.
Proc. Amer. Math. Soc., 111:523–531, 1991.
[69] Netscape Communications Corporation. Potential Vulnerability in
Netscape Products. Available on the WWW at
http://www.netscape.com/newsref/std/random_seed_security.html.
[70] H. Niederreiter. Random Number Generation and Quasi-Monte Carlo
Methods. SIAM, Philadelphia, USA, 1992.
[71] H. Niederreiter. On a new class of pseudorandom numbers for simulation
methods. J. Comput. Appl. Math., 56:159–167, 1994.
[72] H. Niederreiter. New developments in uniform pseudorandom number
and vector generation. In H. Niederreiter and P.J.-S. Shiue, editors, Monte
Carlo and Quasi-Monte Carlo Methods in Scientific Computing, volume 106
of Lecture Notes in Statistics. Springer-Verlag, Heidelberg New York, 1995.
[73] S.K. Park and K.W. Miller. Random number generators: good ones are
hard to find. Comm. ACM, 31:1192–1201, 1988.
[74] C. A. Pickover. Random number generators: pretty good ones are easy
to find. The Visual Computer, 11:369–377, 1995.
[75] B. D. Ripley. Stochastic Simulation. John Wiley, New York, 1987.
[76] R. A. Rueppel. Stream Ciphers. In Gustavus J. Simmons, editor,
Contemporary cryptology: the science of information integrity, chapter 2.
IEEE Press, 1992.
[77] Bruce Schneier. Applied Cryptography. John Wiley & Sons, Inc., first
edition, 1993.
[78] I.M. Sobol. Die Monte-Carlo-Methode. VEB Deutscher Verlag der
Wissenschaften, 1983.
[79] H. Stegbuchner. Zur quantitativen Theorie der Gleichverteilung mod
1. Arbeitsberichte, Mathematisches Institut der Universität Salzburg,
Salzburg, Austria, 1980.
[80] O. Strauch.
discrepancy. Math. Slovaca, 44:601–632, 1994.
[81] R.C. Tausworthe. Random numbers generated by linear recurrence
modulo two. Math. Comp., 19:201–209, 1965.
[82] S. Tezuka. Uniform Random Numbers: Theory and Practice. Kluwer
Academic Publ., 1995.
[83] S. Tezuka and M. Fushimi. Calculation of Fibonacci polynomials for
GFSR sequences with low discrepancies. Math. Comp., 60:763–770, 1993.
[84] J.F. Traub and H. Woźniakowski. The Monte Carlo algorithm with a
pseudorandom generator. Math. Comp., 58:323–339, 1992.
[85] S. Wegenkittl. Empirical Testing of Pseudorandom Number Generators.
Master’s thesis, Institut für Mathematik, Universität Salzburg, Austria,
1995.
[86] S. Wegenkittl.
On empirical testing of pseudorandom number generators. In G. De Pietro,
A. Giordano, M. Vajteršic, and P. Zinterhof, editors, Proceedings of the
International Workshop Parallel Numerics 95, Sorrento, Italy, September
27–29, 1995, pages 113–123. IRSIP Institute of the NRC of Italy, Naples,
1995.
[87] A. Weingartner. Nonlinear congruential pseudorandom number
generators. Master’s thesis, Universität Salzburg, Austria, 1994.
[88] B.A. Wichmann and I.D. Hill. An efficient and portable pseudo-random
number generator. Appl. Statist., 31:188–190, 1982. Corrections, ibid. 33,
123 (1994).
[89] P. Winker and Kai-Tai Fang. Application of threshold accepting to the
evaluation of the discrepancy of a set of points. Research report, Universität
Konstanz, Germany, 1995.
[90] P. Zinterhof. Über einige Abschätzungen bei der Approximation von
Funktionen mit Gleichverteilungsmethoden. Sitzungsber. Österr. Akad.
Wiss. Math.-Natur. Kl. II, 185:121–132, 1976.
Curriculum vitae
Name: Otmar Lendl
Date of birth: May 8th, 1970
Place of birth: Salzburg, Austria
Parents: Ingeborg and Wolfgang Lendl
Education:
| 1976–1980: | Volksschule in Salzburg |
| 1980–1988: | Gymnasium in Salzburg |
| 1988–1996: | University studies (M.Sc. in Mathematics) |
| | at the University of Salzburg |